Block Randomized Optimization for Adaptive Hypergraph Learning

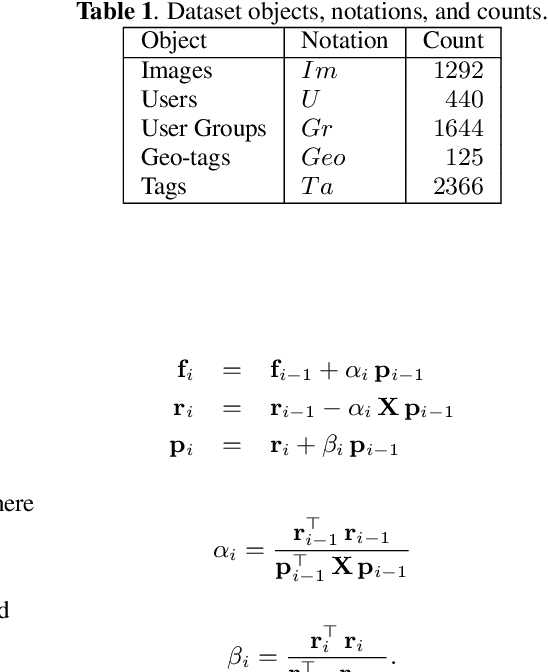
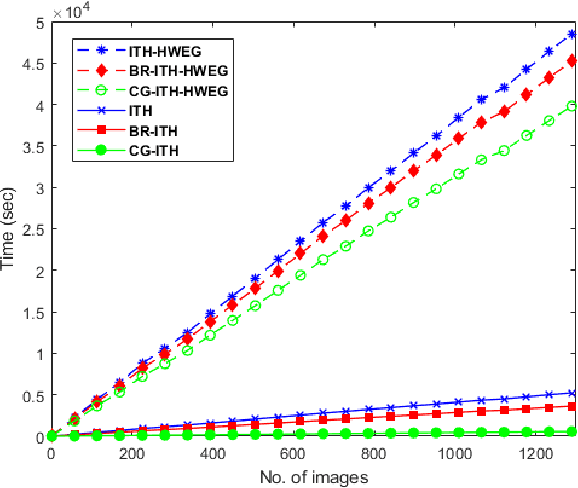
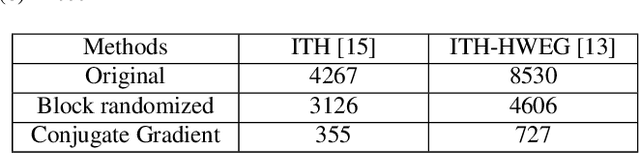
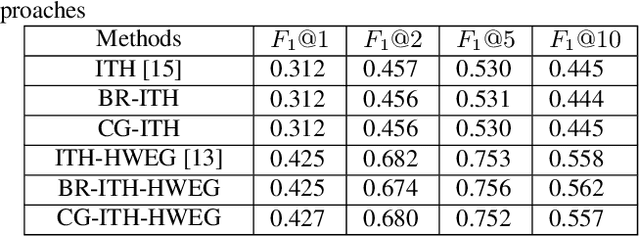
The high-order relations between the content in social media sharing platforms are frequently modeled by a hypergraph. Either hypergraph Laplacian matrix or the adjacency matrix is a big matrix. Randomized algorithms are used for low-rank factorizations in order to approximately decompose and eventually invert such big matrices fast. Here, block randomized Singular Value Decomposition (SVD) via subspace iteration is integrated within adaptive hypergraph weight estimation for image tagging, as a first approach. Specifically, creating low-rank submatrices along the main diagonal by tessellation permits fast matrix inversions via randomized SVD. Moreover, a second approach is proposed for solving the linear system in the optimization problem of hypergraph learning by employing the conjugate gradient method. Both proposed approaches achieve high accuracy in image tagging measured by F1 score and succeed to reduce the computational requirements of adaptive hypergraph weight estimation.