Blind Exploration and Exploitation of Stochastic Experts
Paper and Code
Apr 02, 2021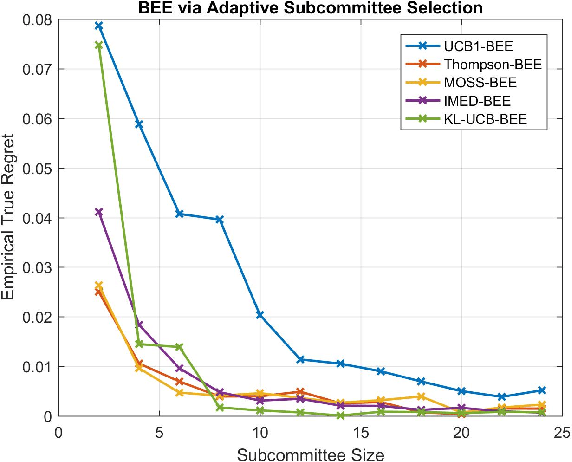

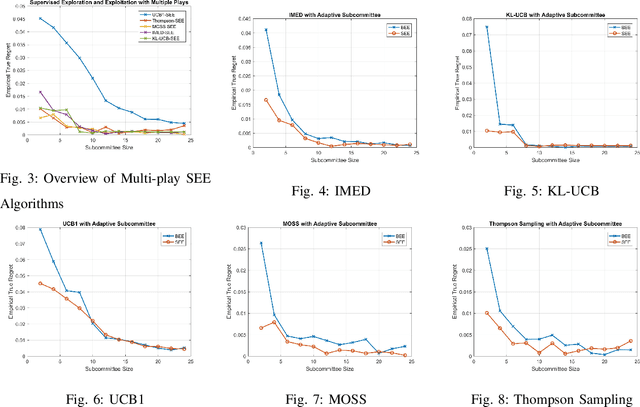
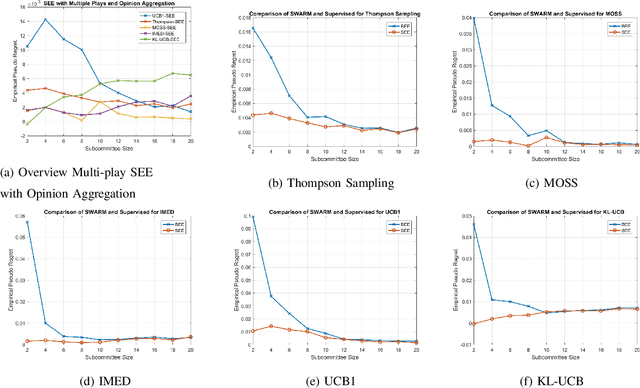
We present blind exploration and exploitation (BEE) algorithms for identifying the most reliable stochastic expert based on formulations that employ posterior sampling, upper-confidence bounds, empirical Kullback-Leibler divergence, and minmax methods for the stochastic multi-armed bandit problem. Joint sampling and consultation of experts whose opinions depend on the hidden and random state of the world becomes challenging in the unsupervised, or blind, framework as feedback from the true state is not available. We propose an empirically realizable measure of expert competence that can be inferred instantaneously using only the opinions of other experts. This measure preserves the ordering of true competences and thus enables joint sampling and consultation of stochastic experts based on their opinions on dynamically changing tasks. Statistics derived from the proposed measure is instantaneously available allowing both blind exploration-exploitation and unsupervised opinion aggregation. We discuss how the lack of supervision affects the asymptotic regret of BEE architectures that rely on UCB1, KL-UCB, MOSS, IMED, and Thompson sampling. We demonstrate the performance of different BEE algorithms empirically and compare them to their standard, or supervised, counterparts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge