Bisimulations for fuzzy transition systems
Paper and Code
Dec 10, 2010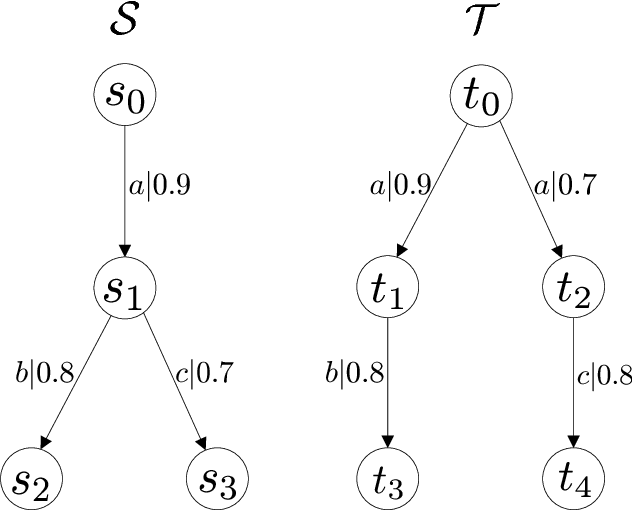
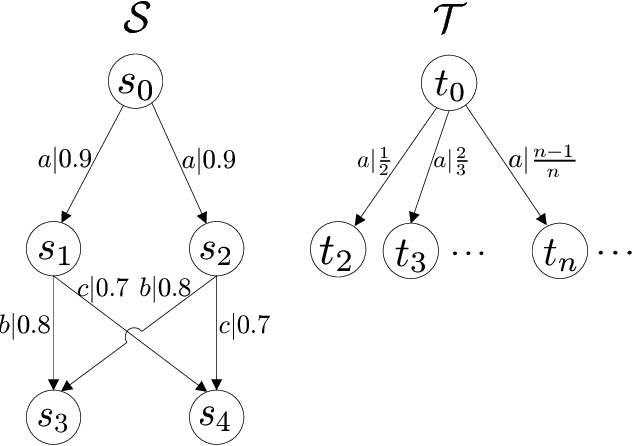
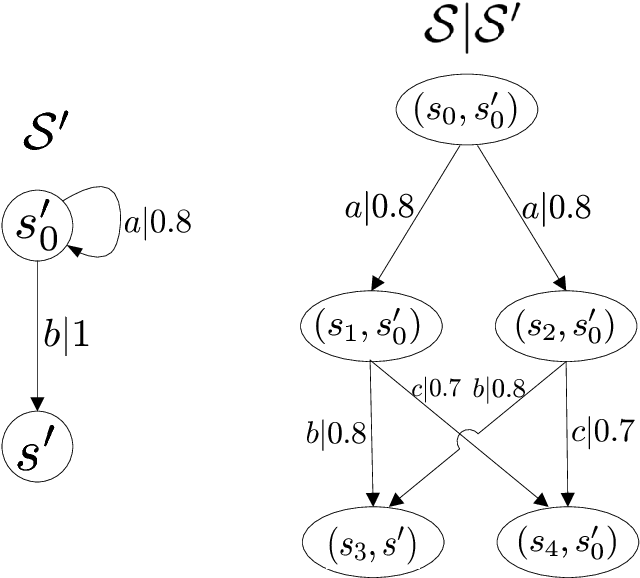
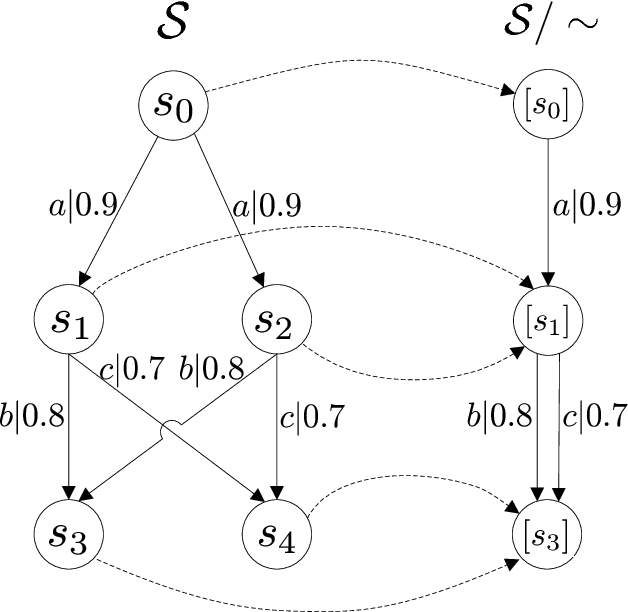
There has been a long history of using fuzzy language equivalence to compare the behavior of fuzzy systems, but the comparison at this level is too coarse. Recently, a finer behavioral measure, bisimulation, has been introduced to fuzzy finite automata. However, the results obtained are applicable only to finite-state systems. In this paper, we consider bisimulation for general fuzzy systems which may be infinite-state or infinite-event, by modeling them as fuzzy transition systems. To help understand and check bisimulation, we characterize it in three ways by enumerating whole transitions, comparing individual transitions, and using a monotonic function. In addition, we address composition operations, subsystems, quotients, and homomorphisms of fuzzy transition systems and discuss their properties connected with bisimulation. The results presented here are useful for comparing the behavior of general fuzzy systems. In particular, this makes it possible to relate an infinite fuzzy system to a finite one, which is easier to analyze, with the same behavior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge