BikNN: Anomaly Estimation in Bilateral Domains with k-Nearest Neighbors
Paper and Code
May 11, 2021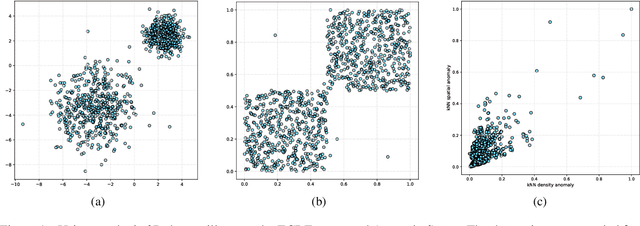
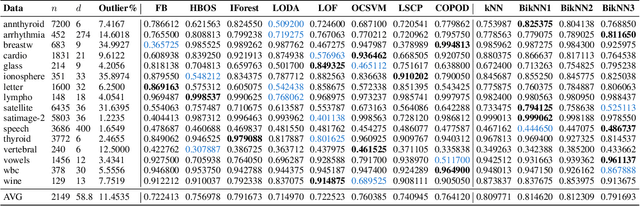
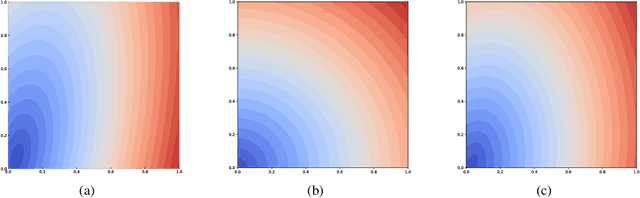
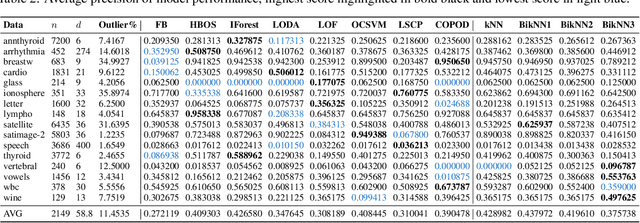
In this paper, a novel framework for anomaly estimation is proposed. The basic idea behind our method is to reduce the data into a two-dimensional space and then rank each data point in the reduced space. We attempt to estimate the degree of anomaly in both spatial and density domains. Specifically, we transform the data points into a density space and measure the distances in density domain between each point and its k-Nearest Neighbors in spatial domain. Then, an anomaly coordinate system is built by collecting two unilateral anomalies from k-nearest neighbors of each point. Further more, we introduce two schemes to model their correlation and combine them to get the final anomaly score. Experiments performed on the synthetic and real world datasets demonstrate that the proposed method performs well and achieve highest average performance. We also show that the proposed method can provide visualization and classification of the anomalies in a simple manner. Due to the complexity of the anomaly, none of the existing methods can perform best on all benchmark datasets. Our method takes into account both the spatial domain and the density domain and can be adapted to different datasets by adjusting a few parameters manually.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge