Belief-State Query Policies for Planning With Preferences Under Partial Observability
Paper and Code
May 24, 2024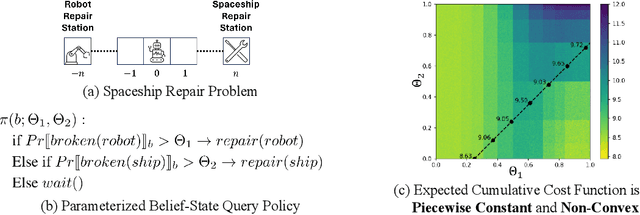
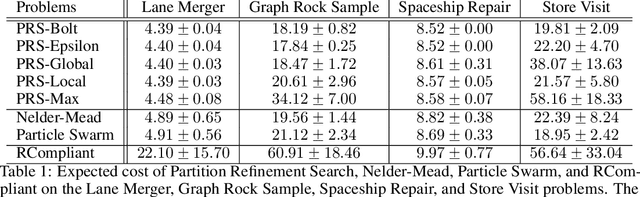
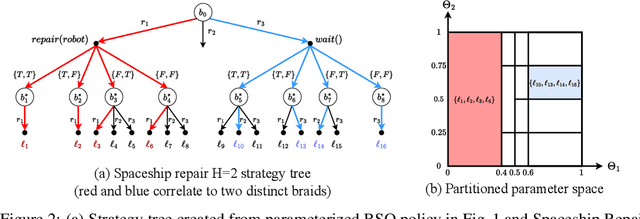
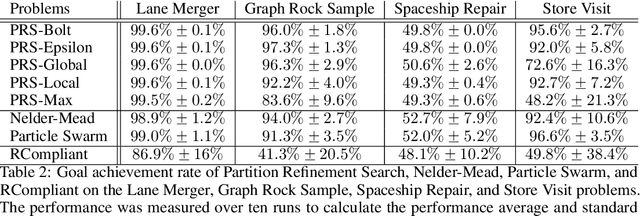
Planning in real-world settings often entails addressing partial observability while aligning with users' preferences. We present a novel framework for expressing users' preferences about agent behavior in a partially observable setting using parameterized belief-state query (BSQ) preferences in the setting of goal-oriented partially observable Markov decision processes (gPOMDPs). We present the first formal analysis of such preferences and prove that while the expected value of a BSQ preference is not a convex function w.r.t its parameters, it is piecewise constant and yields an implicit discrete parameter search space that is finite for finite horizons. This theoretical result leads to novel algorithms that optimize gPOMDP agent behavior while guaranteeing user preference compliance. Theoretical analysis proves that our algorithms converge to the optimal preference-compliant behavior in the limit. Empirical results show that BSQ preferences provide a computationally feasible approach for planning with preferences in partially observable settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge