Beam Search for Learning a Deep Convolutional Neural Network of 3D Shapes
Paper and Code
Dec 14, 2016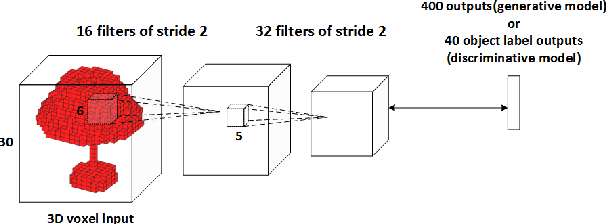
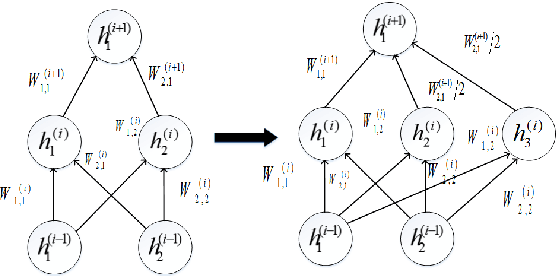
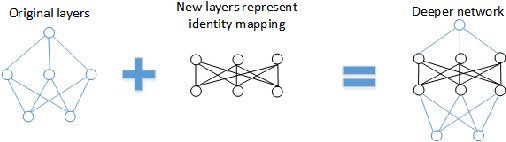
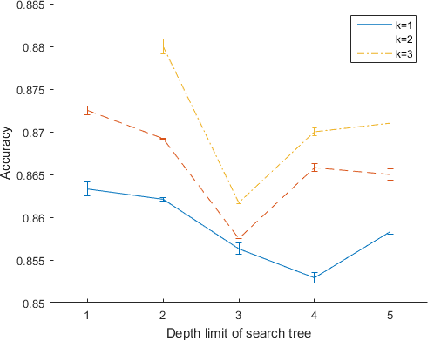
This paper addresses 3D shape recognition. Recent work typically represents a 3D shape as a set of binary variables corresponding to 3D voxels of a uniform 3D grid centered on the shape, and resorts to deep convolutional neural networks(CNNs) for modeling these binary variables. Robust learning of such CNNs is currently limited by the small datasets of 3D shapes available, an order of magnitude smaller than other common datasets in computer vision. Related work typically deals with the small training datasets using a number of ad hoc, hand-tuning strategies. To address this issue, we formulate CNN learning as a beam search aimed at identifying an optimal CNN architecture, namely, the number of layers, nodes, and their connectivity in the network, as well as estimating parameters of such an optimal CNN. Each state of the beam search corresponds to a candidate CNN. Two types of actions are defined to add new convolutional filters or new convolutional layers to a parent CNN, and thus transition to children states. The utility function of each action is efficiently computed by transferring parameter values of the parent CNN to its children, thereby enabling an efficient beam search. Our experimental evaluation on the 3D ModelNet dataset demonstrates that our model pursuit using the beam search yields a CNN with superior performance on 3D shape classification than the state of the art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge