Bayesian vs. PAC-Bayesian Deep Neural Network Ensembles

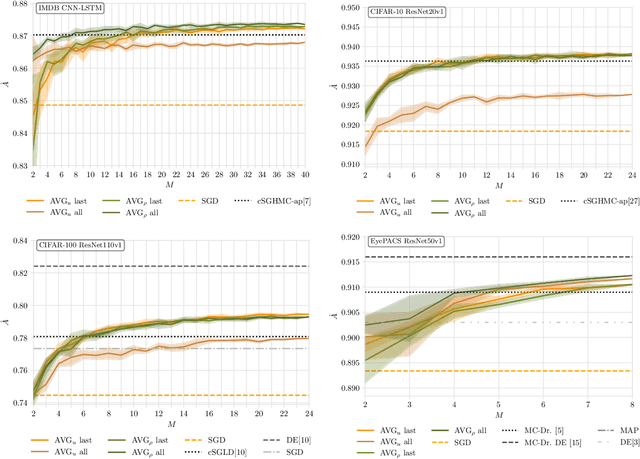
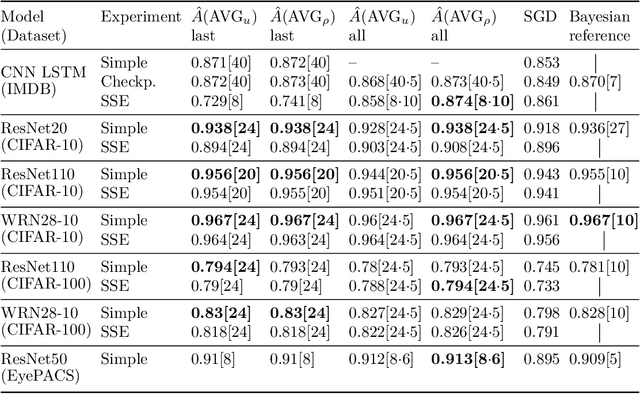
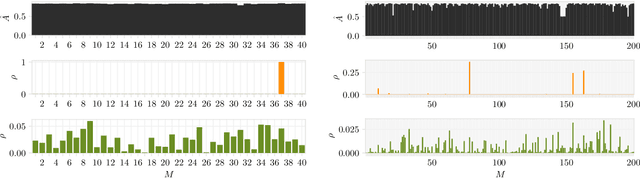
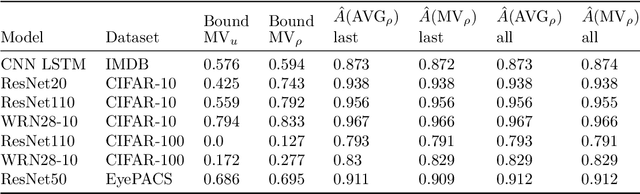
Bayesian neural networks address epistemic uncertainty by learning a posterior distribution over model parameters. Sampling and weighting networks according to this posterior yields an ensemble model referred to as Bayes ensemble. Ensembles of neural networks (deep ensembles) can profit from the cancellation of errors effect: Errors by ensemble members may average out and the deep ensemble achieves better predictive performance than each individual network. We argue that neither the sampling nor the weighting in a Bayes ensemble are particularly well-suited for increasing generalization performance, as they do not support the cancellation of errors effect, which is evident in the limit from the Bernstein-von~Mises theorem for misspecified models. In contrast, a weighted average of models where the weights are optimized by minimizing a PAC-Bayesian generalization bound can improve generalization performance. This requires that the optimization takes correlations between models into account, which can be achieved by minimizing the tandem loss at the cost that hold-out data for estimating error correlations need to be available. The PAC-Bayesian weighting increases the robustness against correlated models and models with lower performance in an ensemble. This allows us to safely add several models from the same learning process to an ensemble, instead of using early-stopping for selecting a single weight configuration. Our study presents empirical results supporting these conceptual considerations on four different classification datasets. We show that state-of-the-art Bayes ensembles from the literature, despite being computationally demanding, do not improve over simple uniformly weighted deep ensembles and cannot match the performance of deep ensembles weighted by optimizing the tandem loss, which additionally come with non-vacuous generalization guarantees.