Bayesian Optimization using Pseudo-Points
Paper and Code
Oct 12, 2019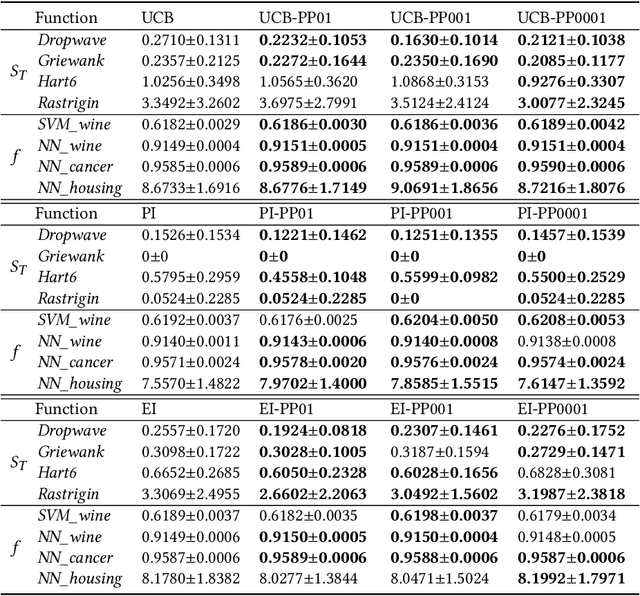
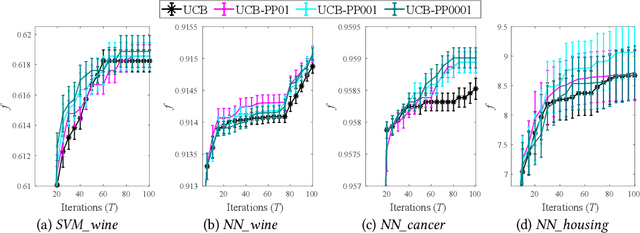
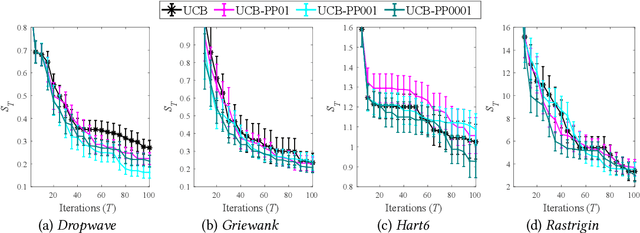
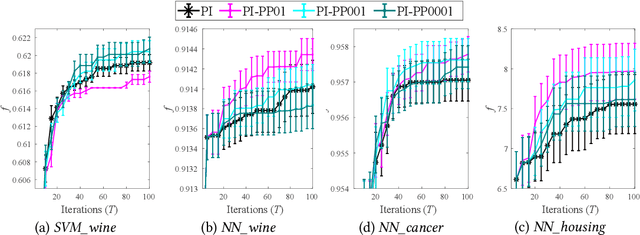
Bayesian optimization (BO) is a popular approach for expensive black-box optimization, with applications in parameter tuning, experimental design, robotics, and so on. BO usually models the objective function by a Gaussian process (GP), and iteratively samples the next data point by maximizing some acquisition function. In this paper, we propose a new general framework for BO by generating pseudo-points (i.e., data points whose objective values are not evaluated) to improve the GP model. With the classic acquisition function, i.e., upper confidence bound (UCB), we prove a general bound on the cumulative regret, and show that the generation of pseudo-points can improve the instantaneous regret. Experiments using UCB and other acquisition functions, i.e., probability of improvement (PI) and expectation of improvement (EI), on synthetic as well as real-world problems clearly show the advantage of generating pseudo-points.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge