Bayesian Optimization for Multi-objective Optimization and Multi-point Search
Paper and Code
May 07, 2019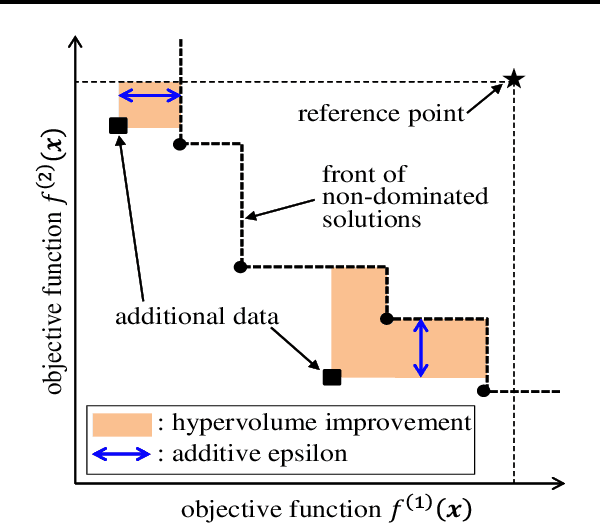

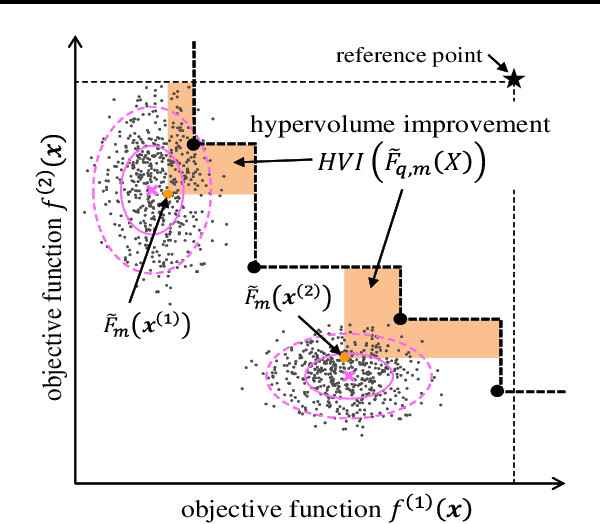
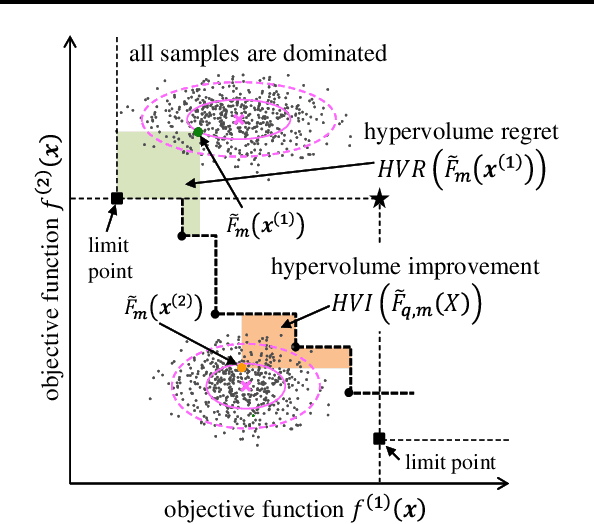
Bayesian optimization is an effective method to efficiently optimize unknown objective functions with high evaluation costs. Traditional Bayesian optimization algorithms select one point per iteration for single objective function, whereas in recent years, Bayesian optimization for multi-objective optimization or multi-point search per iteration have been proposed. However, Bayesian optimization that can deal with them at the same time in non-heuristic way is not known at present. We propose a Bayesian optimization algorithm that can deal with multi-objective optimization and multi-point search at the same time. First, we define an acquisition function that considers both multi-objective and multi-point search problems. It is difficult to analytically maximize the acquisition function as the computational cost is prohibitive even when approximate calculations such as sampling approximation are performed; therefore, we propose an accurate and computationally efficient method for estimating gradient of the acquisition function, and develop an algorithm for Bayesian optimization with multi-objective and multi-point search. It is shown via numerical experiments that the performance of the proposed method is comparable or superior to those of heuristic methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge