Bayesian optimization for backpropagation in Monte-Carlo tree search
Paper and Code
Jan 25, 2020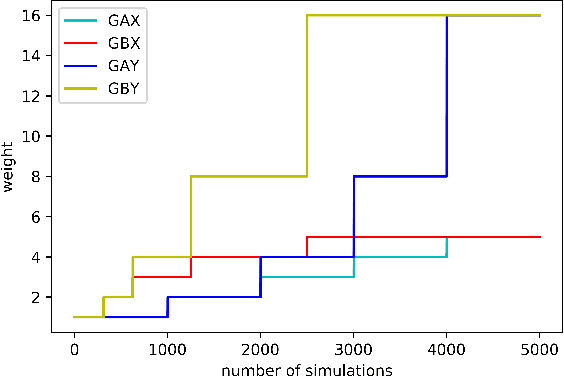

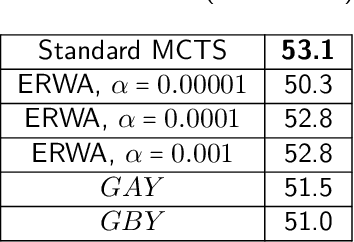
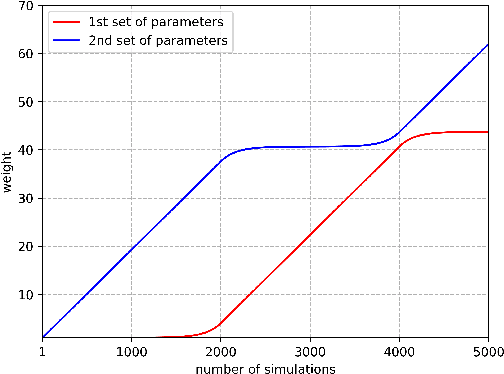
In large domains, Monte-Carlo tree search (MCTS) is required to estimate the values of the states as efficiently and accurately as possible. However, the standard update rule in backpropagation assumes a stationary distribution for the returns, and particularly in min-max trees, convergence to the true value can be slow because of averaging. We present two methods, Softmax MCTS and Monotone MCTS, which generalize previous attempts to improve upon the backpropagation strategy. We demonstrate that both methods reduce to finding optimal monotone functions, which we do so by performing Bayesian optimization with a Gaussian process (GP) prior. We conduct experiments on computer Go, where the returns are given by a deep value neural network, and show that our proposed framework outperforms previous methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge