Bayesian Optimisation for Constrained Problems
Paper and Code
May 27, 2021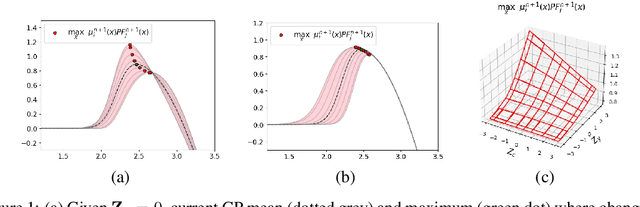
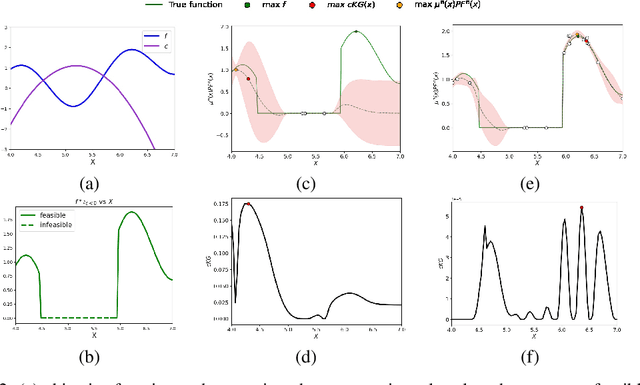
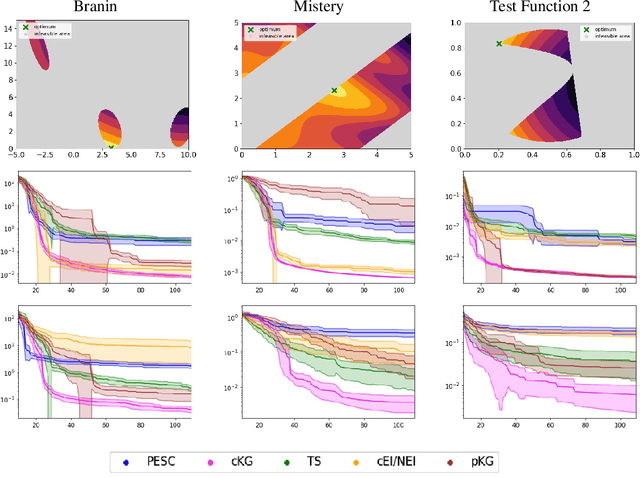
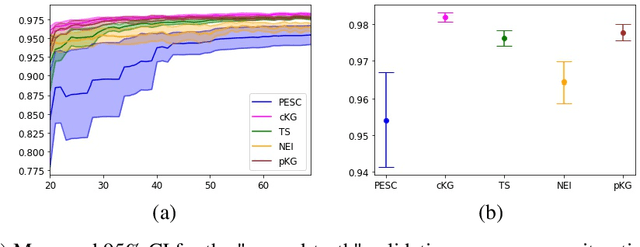
Many real-world optimisation problems such as hyperparameter tuning in machine learning or simulation-based optimisation can be formulated as expensive-to-evaluate black-box functions. A popular approach to tackle such problems is Bayesian optimisation (BO), which builds a response surface model based on the data collected so far, and uses the mean and uncertainty predicted by the model to decide what information to collect next. In this paper, we propose a novel variant of the well-known Knowledge Gradient acquisition function that allows it to handle constraints. We empirically compare the new algorithm with four other state-of-the-art constrained Bayesian optimisation algorithms and demonstrate its superior performance. We also prove theoretical convergence in the infinite budget limit.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge