Bayesian Nonlinear Regression using Sums of Simple Functions
Paper and Code
Dec 04, 2023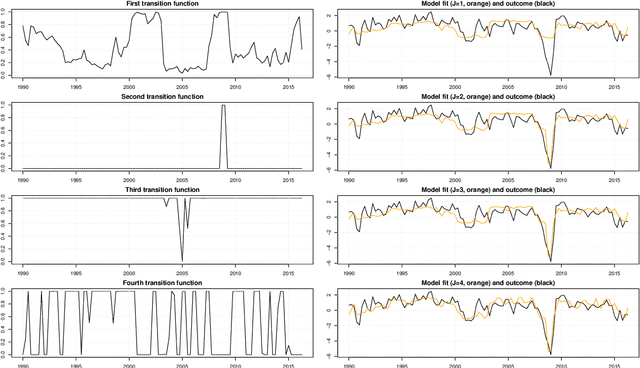
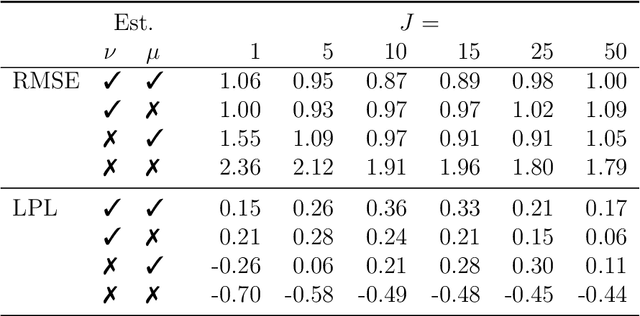
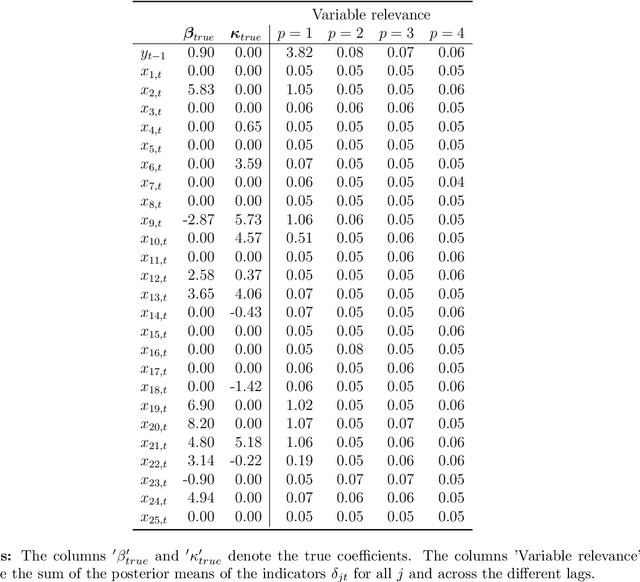
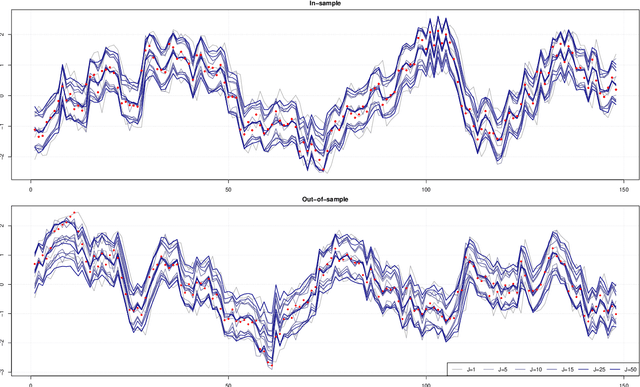
This paper proposes a new Bayesian machine learning model that can be applied to large datasets arising in macroeconomics. Our framework sums over many simple two-component location mixtures. The transition between components is determined by a logistic function that depends on a single threshold variable and two hyperparameters. Each of these individual models only accounts for a minor portion of the variation in the endogenous variables. But many of them are capable of capturing arbitrary nonlinear conditional mean relations. Conjugate priors enable fast and efficient inference. In simulations, we show that our approach produces accurate point and density forecasts. In a real-data exercise, we forecast US macroeconomic aggregates and consider the nonlinear effects of financial shocks in a large-scale nonlinear VAR.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge