Bayesian Networks based Hybrid Quantum-Classical Machine Learning Approach to Elucidate Gene Regulatory Pathways
Paper and Code
Jan 23, 2019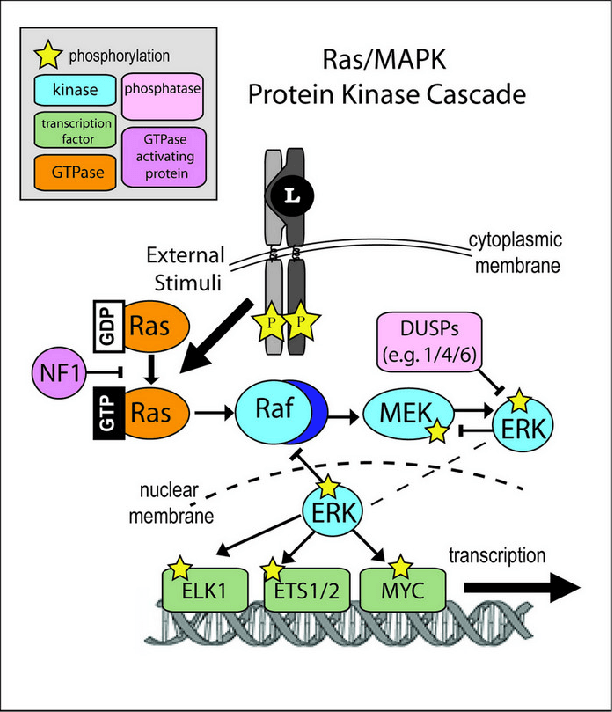
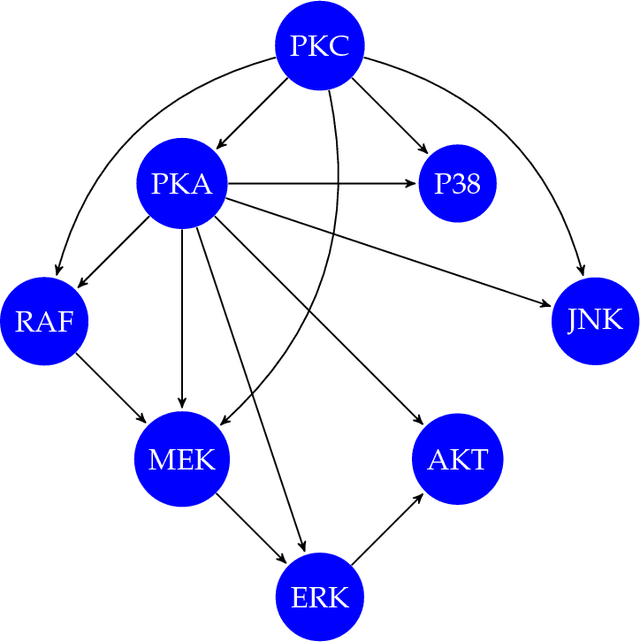
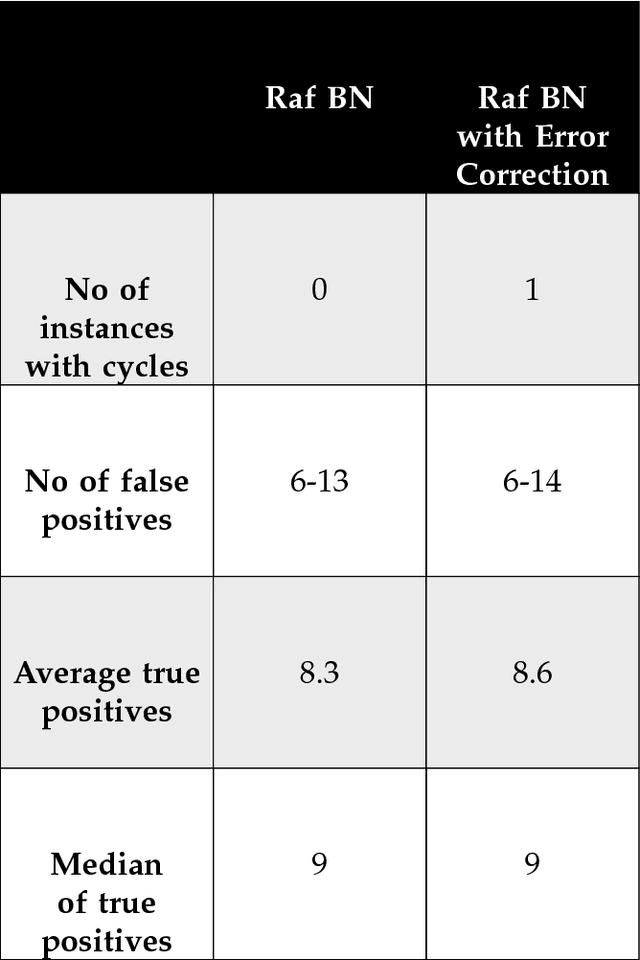
We report a scalable hybrid quantum-classical machine learning framework to build Bayesian networks (BN) that captures the conditional dependence and causal relationships of random variables. The generation of a BN consists of finding a directed acyclic graph (DAG) and the associated joint probability distribution of the nodes consistent with a given dataset. This is a combinatorial problem of structural learning of the underlying graph, starting from a single node and building one arc at a time, that fits a given ensemble using maximum likelihood estimators (MLE). It is cast as an optimization problem that consists of a scoring step performed on a classical computer, penalties for acyclicity and number of parents allowed constraints, and a search step implemented using a quantum annealer. We have assumed uniform priors in deriving the Bayesian network that can be relaxed by formulating the problem as an estimation Dirichlet parameters. We demonstrate the utility of the framework by applying to the problem of elucidating the gene regulatory network for the MAPK/Raf pathway in human T-cells using proteomics data where the concentration of proteins, nodes of the BN, are interpreted as probabilities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge