Bayes Classification using an approximation to the Joint Probability Distribution of the Attributes
Paper and Code
May 29, 2022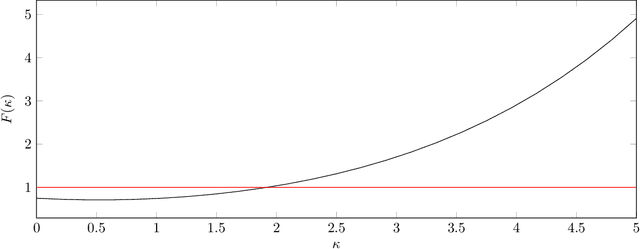
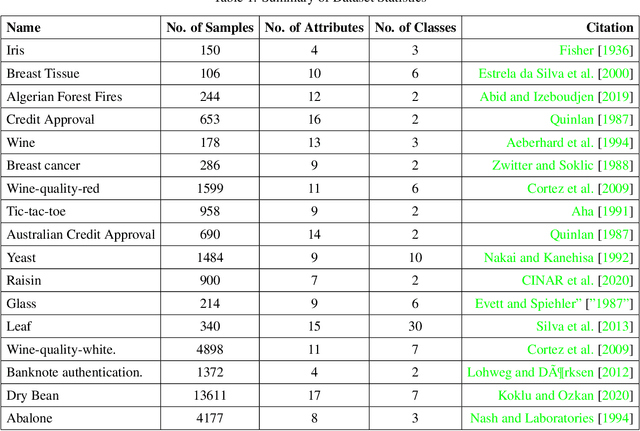
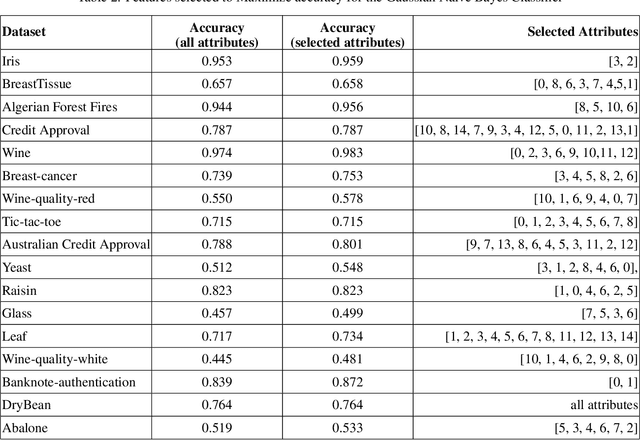
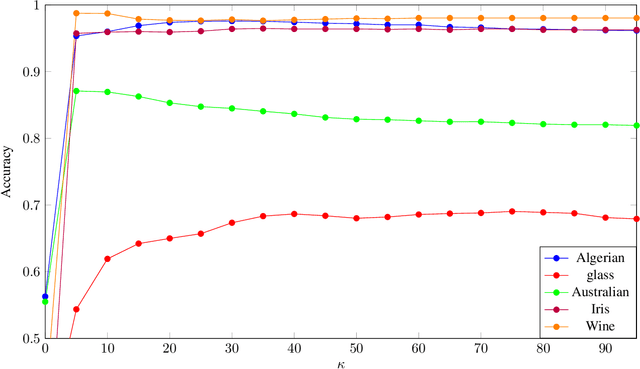
The Naive-Bayes classifier is widely used due to its simplicity, speed and accuracy. However this approach fails when, for at least one attribute value in a test sample, there are no corresponding training samples with that attribute value. This is known as the zero frequency problem and is typically addressed using Laplace Smoothing. However, Laplace Smoothing does not take into account the statistical characteristics of the neighbourhood of the attribute values of the test sample. Gaussian Naive Bayes addresses this but the resulting Gaussian model is formed from global information. We instead propose an approach that estimates conditional probabilities using information in the neighbourhood of the test sample. In this case we no longer need to make the assumption of independence of attribute values and hence consider the joint probability distribution conditioned on the given class which means our approach (unlike the Gaussian and Laplace approaches) takes into consideration dependencies among the attribute values. We illustrate the performance of the proposed approach on a wide range of datasets taken from the University of California at Irvine (UCI) Machine Learning Repository. We also include results for the $k$-NN classifier and demonstrate that the proposed approach is simple, robust and outperforms standard approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge