Baseline Desensitizing In Translation Averaging
Paper and Code
Jan 03, 2019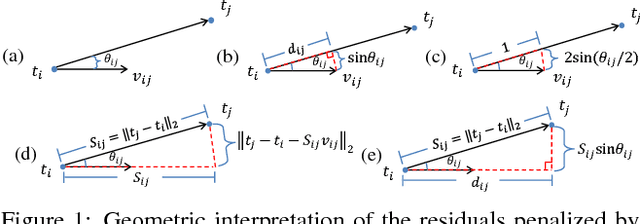
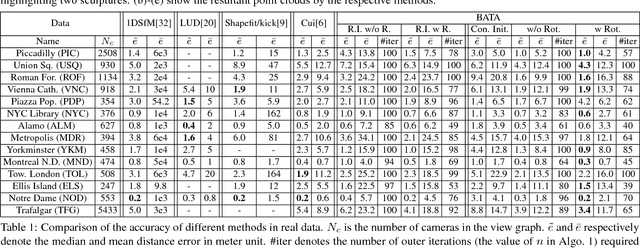
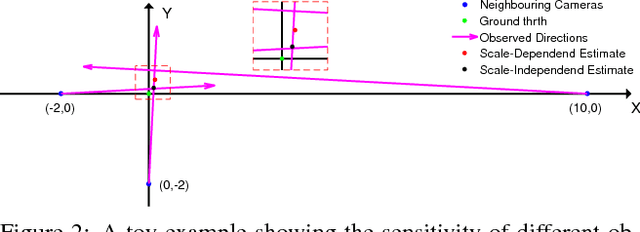
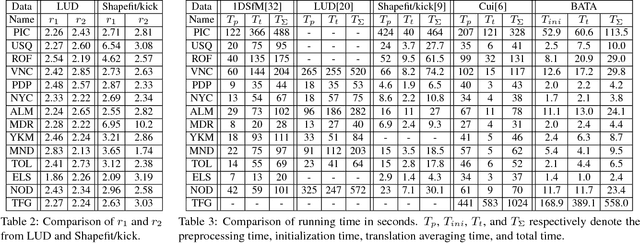
Many existing translation averaging algorithms are either sensitive to disparate camera baselines and have to rely on extensive preprocessing to improve the observed Epipolar Geometry graph, or if they are robust against disparate camera baselines, require complicated optimization to minimize the highly nonlinear angular error objective. In this paper, we carefully design a simple yet effective bilinear objective function, introducing a variable to perform the requisite normalization. The objective function enjoys the baseline-insensitive property of the angular error and yet is amenable to simple and efficient optimization by block coordinate descent, with good empirical performance. A rotation-assisted Iterative Reweighted Least Squares scheme is further put forth to help deal with outliers. We also contribute towards a better understanding of the behavior of two recent convex algorithms, LUD and Shapefit/kick, clarifying the underlying subtle difference that leads to the performance gap. Finally, we demonstrate that our algorithm achieves overall superior accuracies in benchmark dataset compared to state-of-theart methods, and is also several times faster.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge