Band selection with Higher Order Multivariate Cumulants for small target detection in hyperspectral images
Paper and Code
Aug 10, 2018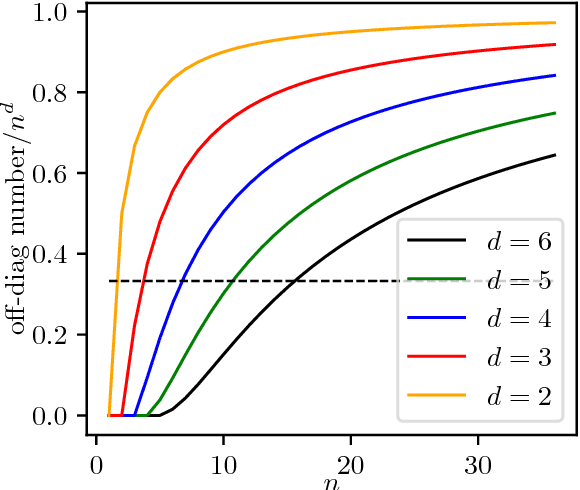

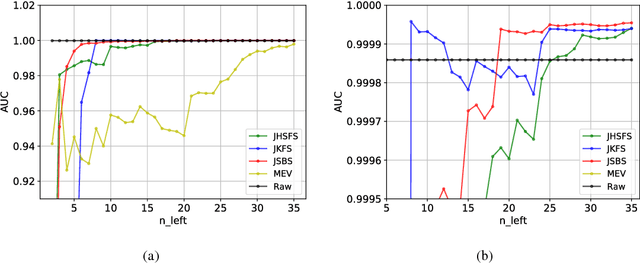
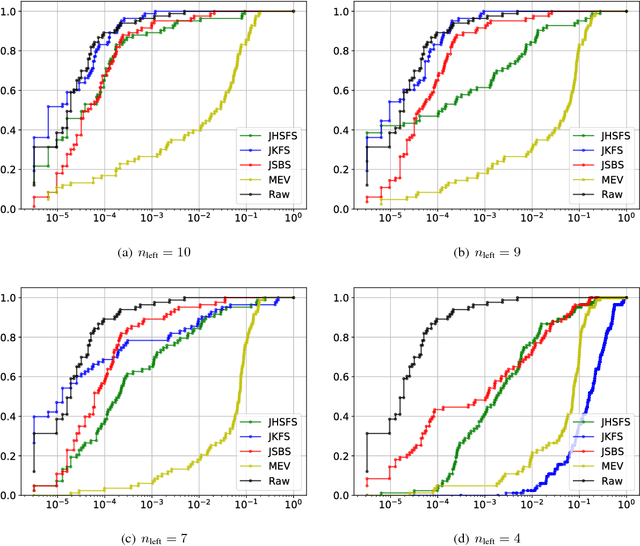
In the small target detection problem a pattern to be located is on the order of magnitude less numerous than other patterns present in the dataset. This applies both to the case of supervised detection, where the known template is expected to match in just a few areas and unsupervised anomaly detection, as anomalies are rare by definition. This problem is frequently related to the imaging applications, i.e. detection within the scene acquired by a camera. To maximize available data about the scene, hyperspectral cameras are used; at each pixel, they record spectral data in hundreds of narrow bands. The typical feature of hyperspectral imaging is that characteristic properties of target materials are visible in the small number of bands, where light of certain wavelength interacts with characteristic molecules. A target-independent band selection method based on statistical principles is a versatile tool for solving this problem in different practical applications. Combination of a regular background and a rare standing out anomaly will produce a distortion in the joint distribution of hyperspectral pixels. Higher Order Cumulants Tensors are a natural `window' into this distribution, allowing to measure properties and suggest candidate bands for removal. While there have been attempts at producing band selection algorithms based on the 3 rd cumulant's tensor i.e. the joint skewness, the literature lacks a systematic analysis of how the order of the cumulant tensor used affects effectiveness of band selection in detection applications. In this paper we present an analysis of a general algorithm for band selection based on higher order cumulants. We discuss its usability related to the observed breaking points in performance, depending both on method order and the desired number of bands. Finally we perform experiments and evaluate these methods in a hyperspectral detection scenario.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge