Avoiding unwanted results in locally linear embedding: A new understanding of regularization
Paper and Code
Aug 28, 2021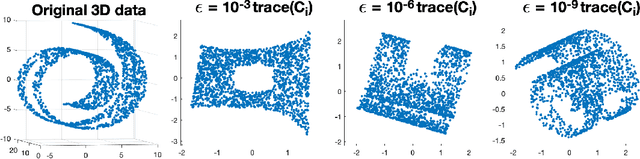
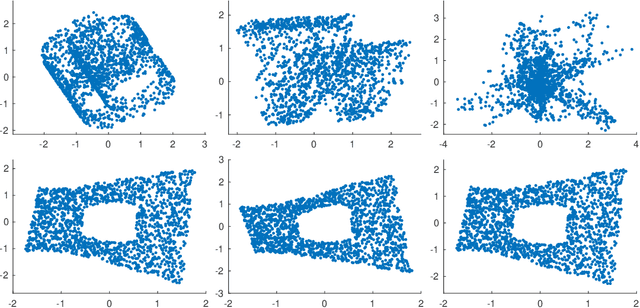
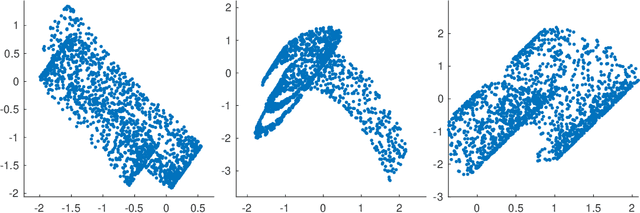
We demonstrate that locally linear embedding (LLE) inherently admits some unwanted results when no regularization is used, even for cases in which regularization is not supposed to be needed in the original algorithm. The existence of one special type of result, which we call ``projection pattern'', is mathematically proved in the situation that an exact local linear relation is achieved in each neighborhood of the data. These special patterns as well as some other bizarre results that may occur in more general situations are shown by numerical examples on the Swiss roll with a hole embedded in a high dimensional space. It is observed that all these bad results can be effectively prevented by using regularization.
* 11 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge