Automatic Differentiation for Adjoint Stencil Loops
Paper and Code
Jul 05, 2019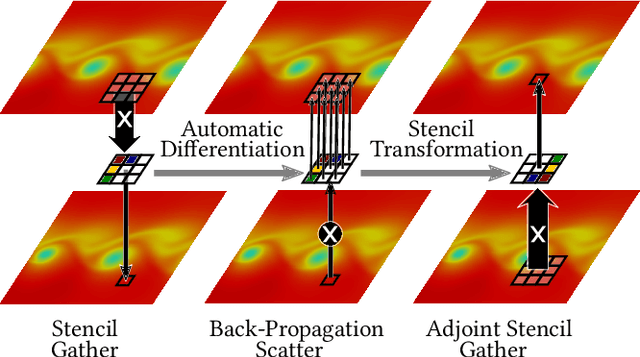

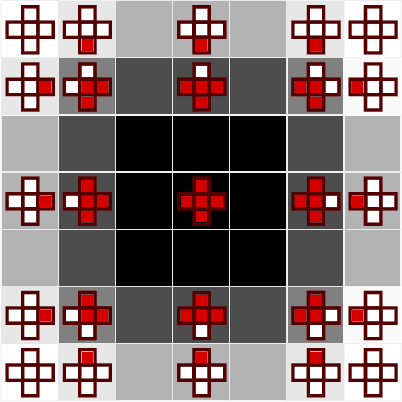

Stencil loops are a common motif in computations including convolutional neural networks, structured-mesh solvers for partial differential equations, and image processing. Stencil loops are easy to parallelise, and their fast execution is aided by compilers, libraries, and domain-specific languages. Reverse-mode automatic differentiation, also known as algorithmic differentiation, autodiff, adjoint differentiation, or back-propagation, is sometimes used to obtain gradients of programs that contain stencil loops. Unfortunately, conventional automatic differentiation results in a memory access pattern that is not stencil-like and not easily parallelisable. In this paper we present a novel combination of automatic differentiation and loop transformations that preserves the structure and memory access pattern of stencil loops, while computing fully consistent derivatives. The generated loops can be parallelised and optimised for performance in the same way and using the same tools as the original computation. We have implemented this new technique in the Python tool PerforAD, which we release with this paper along with test cases derived from seismic imaging and computational fluid dynamics applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge