Autoencoders and Probabilistic Inference with Missing Data: An Exact Solution for The Factor Analysis Case

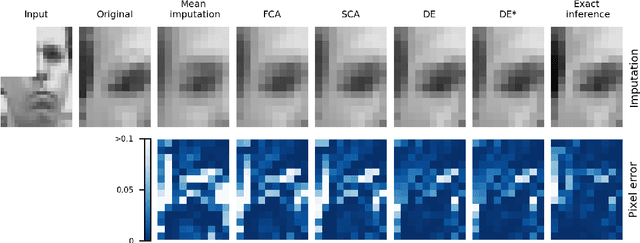
Latent variable models can be used to probabilistically "fill-in" missing data entries. The variational autoencoder architecture (Kingma and Welling, 2014; Rezende et al., 2014) includes a "recognition" or "encoder" network that infers the latent variables given the data variables. However, it is not clear how to handle missing data variables in this network. The factor analysis (FA) model is a basic autoencoder, using linear encoder and decoder networks. We show how to calculate exactly the latent posterior distribution for the factor analysis (FA) model in the presence of missing data, and note that this solution exhibits a non-trivial dependence on the pattern of missingness. We also discuss various approximations to the exact solution. Experiments compare the effectiveness of various approaches to filling in the missing data.