Augmented Message Passing Stein Variational Gradient Descent
Paper and Code
May 18, 2023
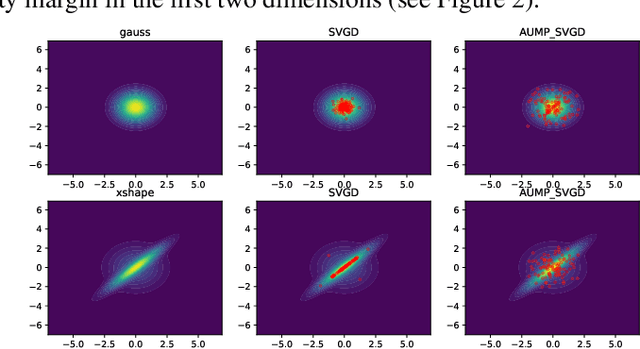

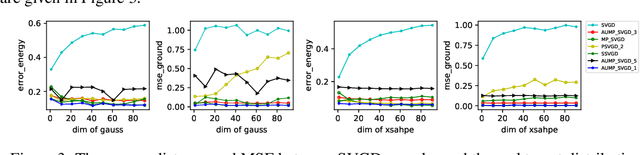
Stein Variational Gradient Descent (SVGD) is a popular particle-based method for Bayesian inference. However, its convergence suffers from the variance collapse, which reduces the accuracy and diversity of the estimation. In this paper, we study the isotropy property of finite particles during the convergence process and show that SVGD of finite particles cannot spread across the entire sample space. Instead, all particles tend to cluster around the particle center within a certain range and we provide an analytical bound for this cluster. To further improve the effectiveness of SVGD for high-dimensional problems, we propose the Augmented Message Passing SVGD (AUMP-SVGD) method, which is a two-stage optimization procedure that does not require sparsity of the target distribution, unlike the MP-SVGD method. Our algorithm achieves satisfactory accuracy and overcomes the variance collapse problem in various benchmark problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge