At-Most-One Constraints in Efficient Representations of Mutex Networks
Paper and Code
Jun 10, 2020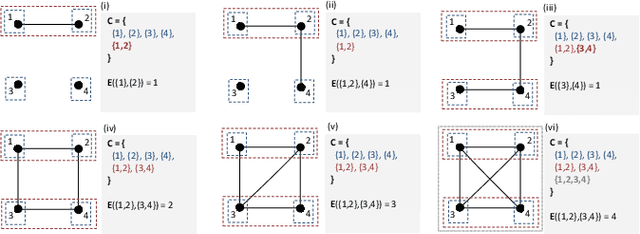
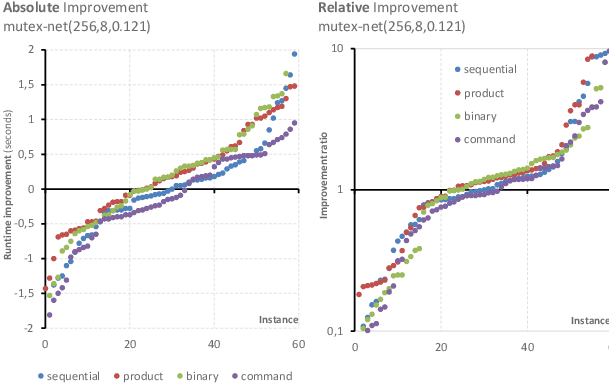
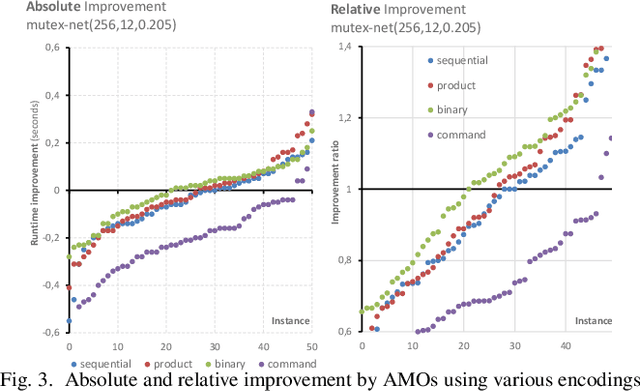
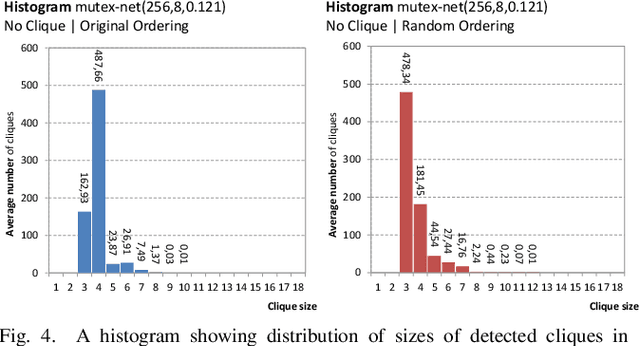
The At-Most-One (AMO) constraint is a special case of cardinality constraint that requires at most one variable from a set of Boolean variables to be set to TRUE. AMO is important for modeling problems as Boolean satisfiability (SAT) from domains where decision variables represent spatial or temporal placements of some objects that cannot share the same spatial or temporal slot. The AMO constraint can be used for more efficient representation and problem solving in mutex networks consisting of pair-wise mutual exclusions forbidding pairs of Boolean variable to be simultaneously TRUE. An on-line method for automated detection of cliques for efficient representation of incremental mutex networks where new mutexes arrive using AMOs is presented. A comparison of SAT-based problem solving in mutex networks represented by AMO constraints using various encodings is shown.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge