Asymptotics of $\ell_2$ Regularized Network Embeddings
Paper and Code
Jan 05, 2022
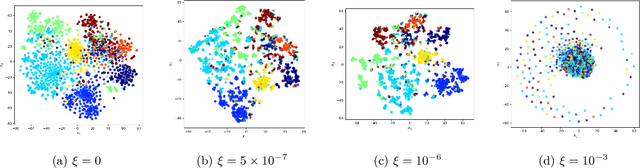
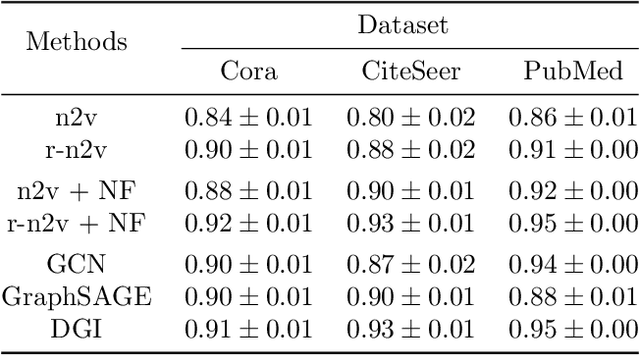
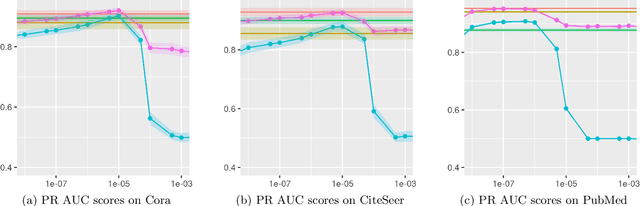
A common approach to solving tasks, such as node classification or link prediction, on a large network begins by learning a Euclidean embedding of the nodes of the network, from which regular machine learning methods can be applied. For unsupervised random walk methods such as DeepWalk and node2vec, adding a $\ell_2$ penalty on the embedding vectors to the loss leads to improved downstream task performance. In this paper we study the effects of this regularization and prove that, under exchangeability assumptions on the graph, it asymptotically leads to learning a nuclear-norm-type penalized graphon. In particular, the exact form of the penalty depends on the choice of subsampling method used within stochastic gradient descent to learn the embeddings. We also illustrate empirically that concatenating node covariates to $\ell_2$ regularized node2vec embeddings leads to comparable, if not superior, performance to methods which incorporate node covariates and the network structure in a non-linear manner.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge