Asymptotic Nash Equilibrium for the $M$-ary Sequential Adversarial Hypothesis Testing Game
Paper and Code
Jun 20, 2022

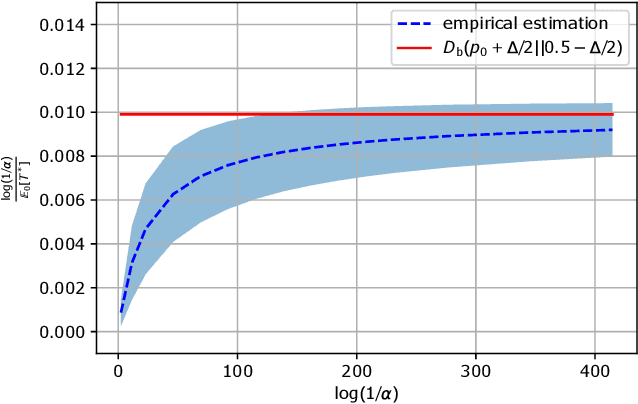
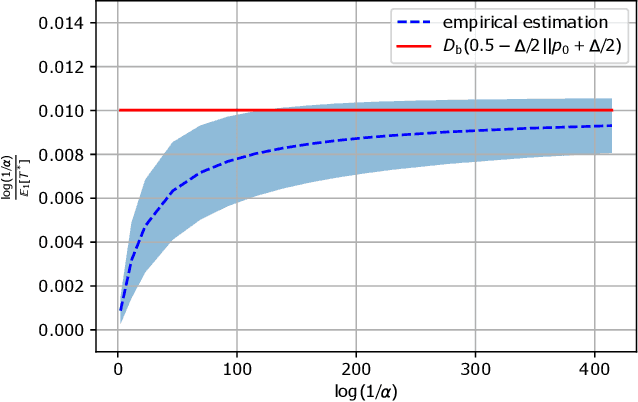
In this paper, we consider a novel $M$-ary sequential hypothesis testing problem in which an adversary is present and perturbs the distributions of the samples before the decision maker observes them. This problem is formulated as a sequential adversarial hypothesis testing game played between the decision maker and the adversary. This game is a zero-sum and strategic one. We assume the adversary is active under \emph{all} hypotheses and knows the underlying distribution of observed samples. We adopt this framework as it is the worst-case scenario from the perspective of the decision maker. The goal of the decision maker is to minimize the expectation of the stopping time to ensure that the test is as efficient as possible; the adversary's goal is, instead, to maximize the stopping time. We derive a pair of strategies under which the asymptotic Nash equilibrium of the game is attained. We also consider the case in which the adversary is not aware of the underlying hypothesis and hence is constrained to apply the same strategy regardless of which hypothesis is in effect. Numerical results corroborate our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge