Asymptotic consistency and order specification for logistic classifier chains in multi-label learning
Paper and Code
Feb 24, 2016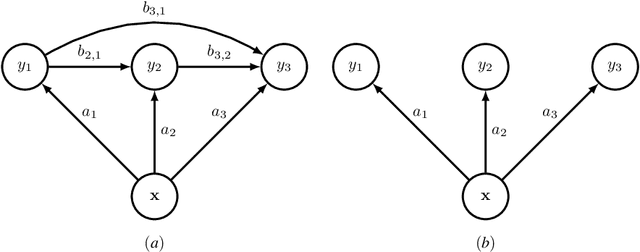
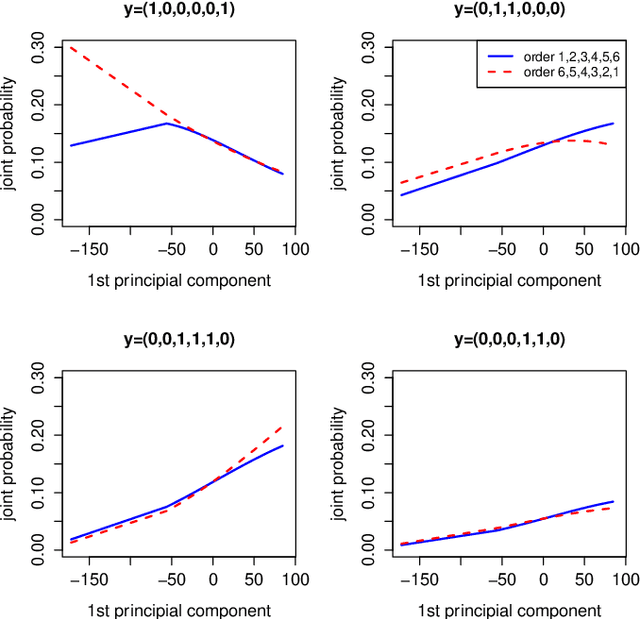
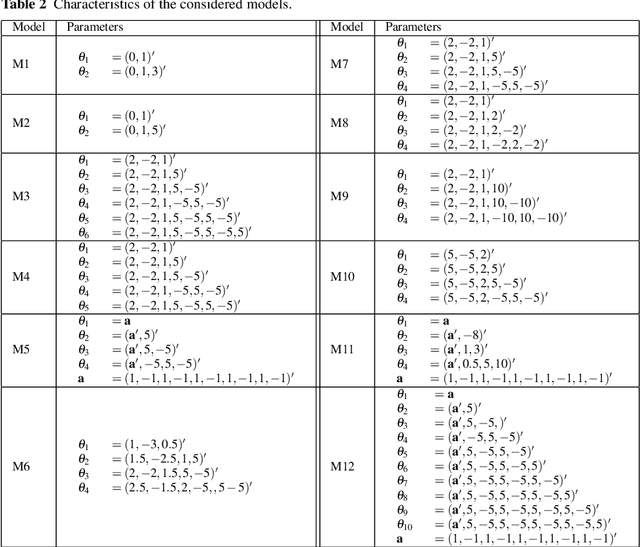
Classifier chains are popular and effective method to tackle a multi-label classification problem. The aim of this paper is to study the asymptotic properties of the chain model in which the conditional probabilities are of the logistic form. In particular we find conditions on the number of labels and the distribution of feature vector under which the estimated mode of the joint distribution of labels converges to the true mode. Best of our knowledge, this important issue has not yet been studied in the context of multi-label learning. We also investigate how the order of model building in a chain influences the estimation of the joint distribution of labels. We establish the link between the problem of incorrect ordering in the chain and incorrect model specification. We propose a procedure of determining the optimal ordering of labels in the chain, which is based on using measures of correct specification and allows to find the ordering such that the consecutive logistic models are best possibly specified. The other important question raised in this paper is how accurately can we estimate the joint posterior probability when the ordering of labels is wrong or the logistic models in the chain are incorrectly specified. The numerical experiments illustrate the theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge