Asymmetric Random Projections
Paper and Code
Jun 22, 2019


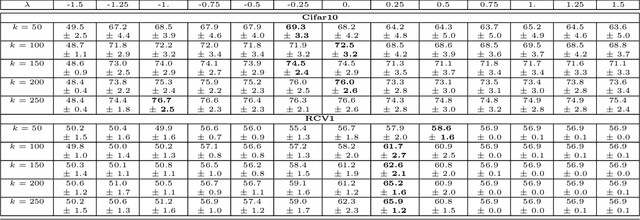
Random projections (RP) are a popular tool for reducing dimensionality while preserving local geometry. In many applications the data set to be projected is given to us in advance, yet the current RP techniques do not make use of information about the data. In this paper, we provide a computationally light way to extract statistics from the data that allows designing a data dependent RP with superior performance compared to data-oblivious RP. We tackle scenarios such as matrix multiplication and linear regression/classification in which we wish to estimate inner products between pairs of vectors from two possibly different sources. Our technique takes advantage of the difference between the sources and is provably superior to oblivious RPs. Additionally, we provide extensive experiments comparing RPs with our approach showing significant performance lifts in fast matrix multiplication, regression and classification problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge