Assessment of Uncertainty Quantification in Universal Differential Equations
Paper and Code
Jun 13, 2024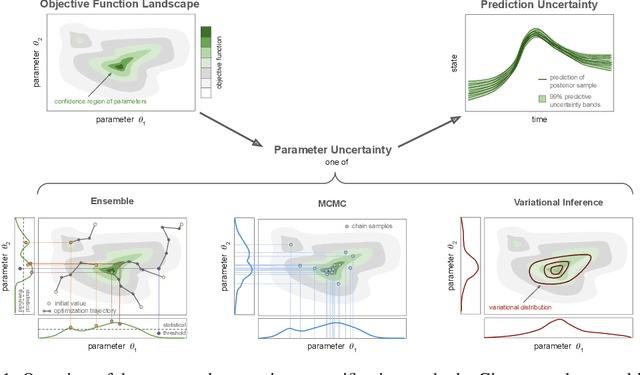
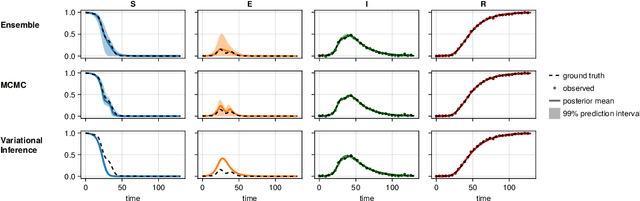
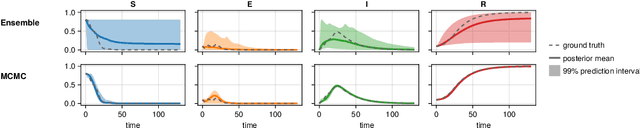
Scientific Machine Learning is a new class of approaches that integrate physical knowledge and mechanistic models with data-driven techniques for uncovering governing equations of complex processes. Among the available approaches, Universal Differential Equations (UDEs) are used to combine prior knowledge in the form of mechanistic formulations with universal function approximators, like neural networks. Integral to the efficacy of UDEs is the joint estimation of parameters within mechanistic formulations and the universal function approximators using empirical data. The robustness and applicability of resultant models, however, hinge upon the rigorous quantification of uncertainties associated with these parameters, as well as the predictive capabilities of the overall model or its constituent components. With this work, we provide a formalisation of uncertainty quantification (UQ) for UDEs and investigate important frequentist and Bayesian methods. By analysing three synthetic examples of varying complexity, we evaluate the validity and efficiency of ensembles, variational inference and Markov chain Monte Carlo sampling as epistemic UQ methods for UDEs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge