Artificial Neural Networks, Symmetries and Differential Evolution
Paper and Code
Apr 08, 2011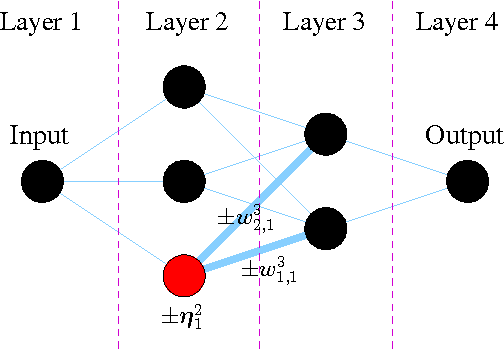
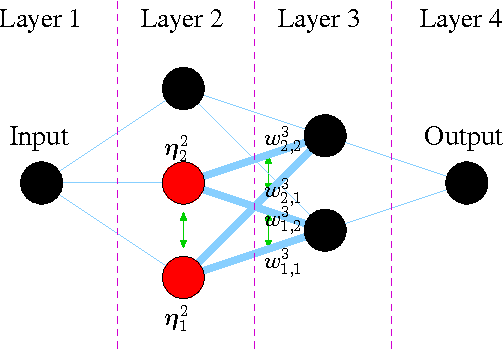
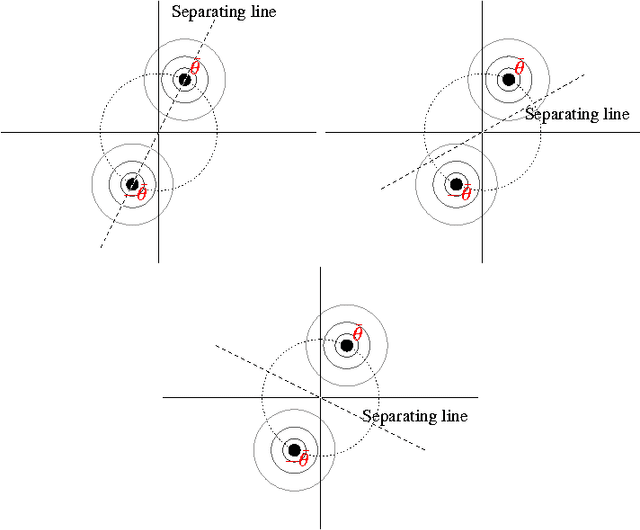
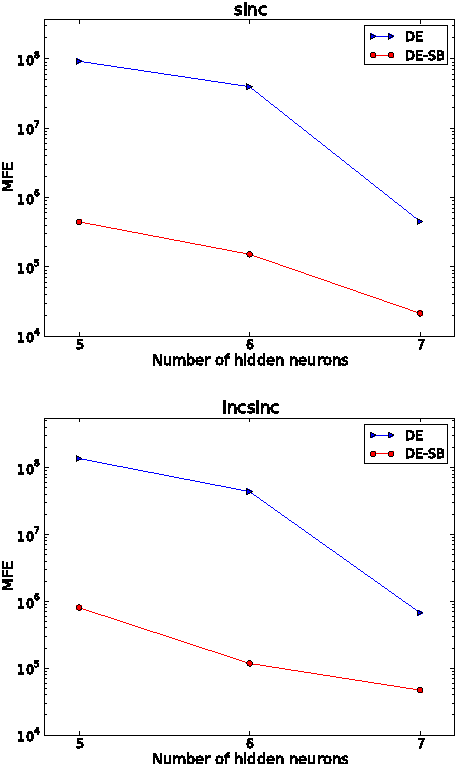
Neuroevolution is an active and growing research field, especially in times of increasingly parallel computing architectures. Learning methods for Artificial Neural Networks (ANN) can be divided into two groups. Neuroevolution is mainly based on Monte-Carlo techniques and belongs to the group of global search methods, whereas other methods such as backpropagation belong to the group of local search methods. ANN's comprise important symmetry properties, which can influence Monte-Carlo methods. On the other hand, local search methods are generally unaffected by these symmetries. In the literature, dealing with the symmetries is generally reported as being not effective or even yielding inferior results. In this paper, we introduce the so called Minimum Global Optimum Proximity principle derived from theoretical considerations for effective symmetry breaking, applied to offline supervised learning. Using Differential Evolution (DE), which is a popular and robust evolutionary global optimization method, we experimentally show significant global search efficiency improvements by symmetry breaking.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge