Approximative Algorithms for Multi-Marginal Optimal Transport and Free-Support Wasserstein Barycenters
Paper and Code
Feb 02, 2022
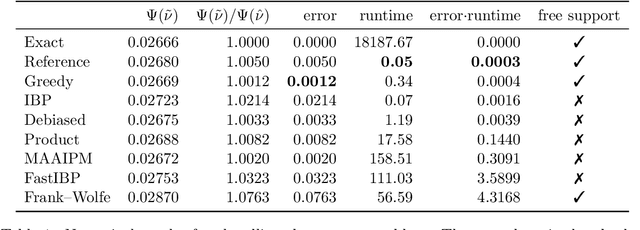
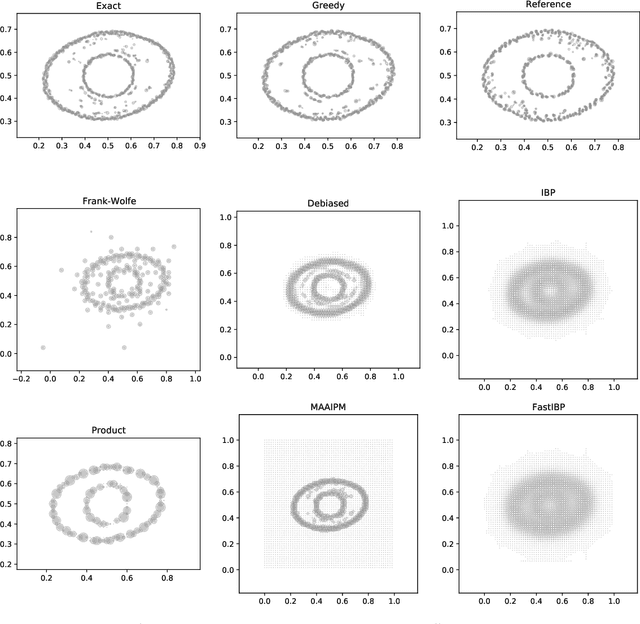
Computationally solving multi-marginal optimal transport (MOT) with squared Euclidean costs for $N$ discrete probability measures has recently attracted considerable attention, in part because of the correspondence of its solutions with Wasserstein-$2$ barycenters, which have many applications in data science. In general, this problem is NP-hard, calling for practical approximative algorithms. While entropic regularization has been successfully applied to approximate Wasserstein barycenters, this loses the sparsity of the optimal solution, making it difficult to solve the MOT problem directly in practice because of the curse of dimensionality. Thus, for obtaining barycenters, one usually resorts to fixed-support restrictions to a grid, which is, however, prohibitive in higher ambient dimensions $d$. In this paper, after analyzing the relationship between MOT and barycenters, we present two algorithms to approximate the solution of MOT directly, requiring mainly just $N-1$ standard two-marginal OT computations. Thus, they are fast, memory-efficient and easy to implement and can be used with any sparse OT solver as a black box. Moreover, they produce sparse solutions and show promising numerical results. We analyze these algorithms theoretically, proving upper and lower bounds for the relative approximation error.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge