Approximation Capabilities of Neural Ordinary Differential Equations
Paper and Code
Jul 30, 2019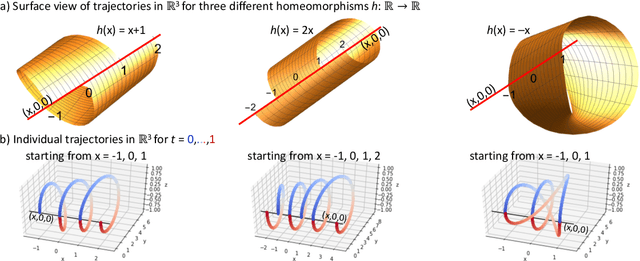
Neural Ordinary Differential Equations have been recently proposed as an infinite-depth generalization of residual networks. Neural ODEs provide out-of-the-box invertibility of the mapping realized by the neural network, and can lead to networks that are more efficient in terms of computational time and parameter space. Here, we show that a Neural ODE operating on a space with dimensionality increased by one compared to the input dimension is a universal approximator for the space of continuous functions, at the cost of loosing invertibility. We then turn our focus to invertible mappings, and we prove that any homeomorphism on a $p$-dimensional Euclidean space can be approximated by a Neural ODE operating on a $(2p+1)$-dimensional Euclidean space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge