Annihilation of Spurious Minima in Two-Layer ReLU Networks
Paper and Code
Oct 12, 2022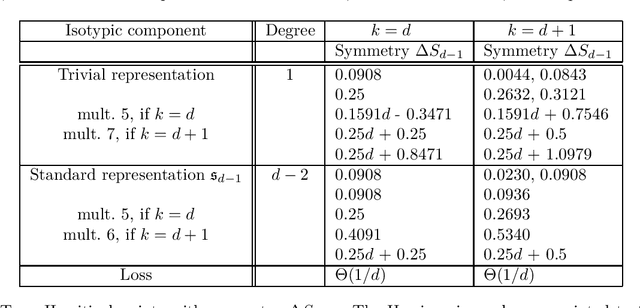
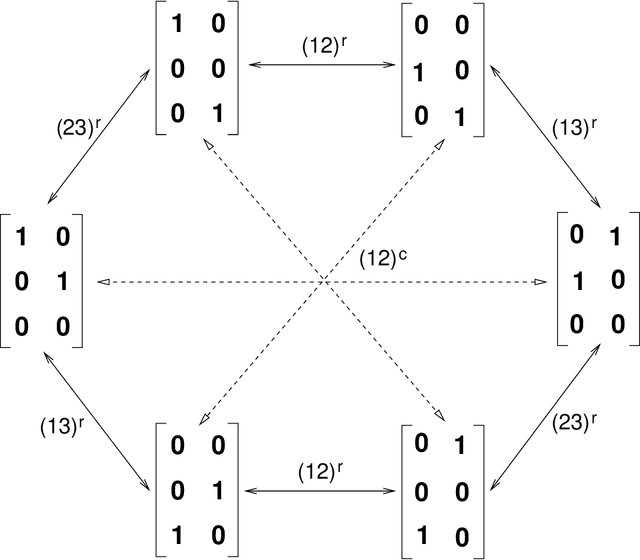
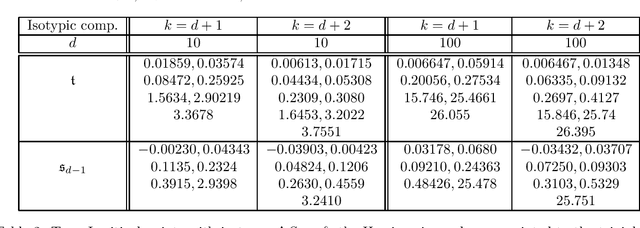
We study the optimization problem associated with fitting two-layer ReLU neural networks with respect to the squared loss, where labels are generated by a target network. Use is made of the rich symmetry structure to develop a novel set of tools for studying the mechanism by which over-parameterization annihilates spurious minima. Sharp analytic estimates are obtained for the loss and the Hessian spectrum at different minima, and it is proved that adding neurons can turn symmetric spurious minima into saddles; minima of lesser symmetry require more neurons. Using Cauchy's interlacing theorem, we prove the existence of descent directions in certain subspaces arising from the symmetry structure of the loss function. This analytic approach uses techniques, new to the field, from algebraic geometry, representation theory and symmetry breaking, and confirms rigorously the effectiveness of over-parameterization in making the associated loss landscape accessible to gradient-based methods. For a fixed number of neurons and inputs, the spectral results remain true under symmetry breaking perturbation of the target.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge