Anisotropic Graph Convolutional Network for Semi-supervised Learning
Paper and Code
Oct 20, 2020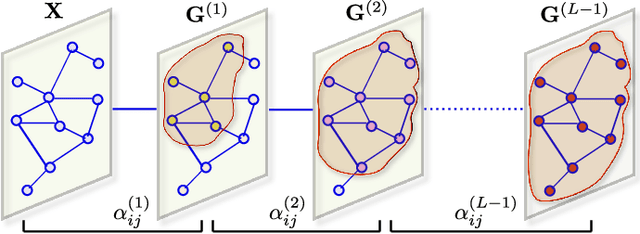
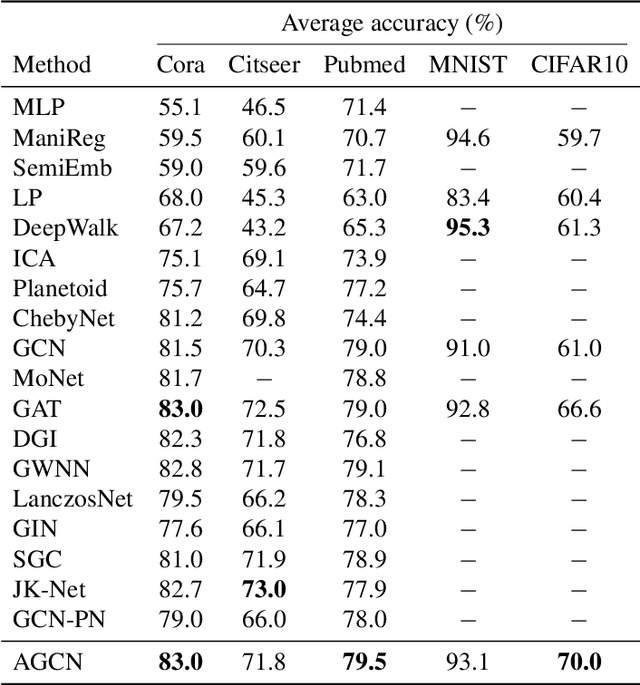


Graph convolutional networks learn effective node embeddings that have proven to be useful in achieving high-accuracy prediction results in semi-supervised learning tasks, such as node classification. However, these networks suffer from the issue of over-smoothing and shrinking effect of the graph due in large part to the fact that they diffuse features across the edges of the graph using a linear Laplacian flow. This limitation is especially problematic for the task of node classification, where the goal is to predict the label associated with a graph node. To address this issue, we propose an anisotropic graph convolutional network for semi-supervised node classification by introducing a nonlinear function that captures informative features from nodes, while preventing oversmoothing. The proposed framework is largely motivated by the good performance of anisotropic diffusion in image and geometry processing, and learns nonlinear representations based on local graph structure and node features. The effectiveness of our approach is demonstrated on three citation networks and two image datasets, achieving better or comparable classification accuracy results compared to the standard baseline methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge