Angular Embedding: A New Angular Robust Principal Component Analysis
Paper and Code
Nov 22, 2020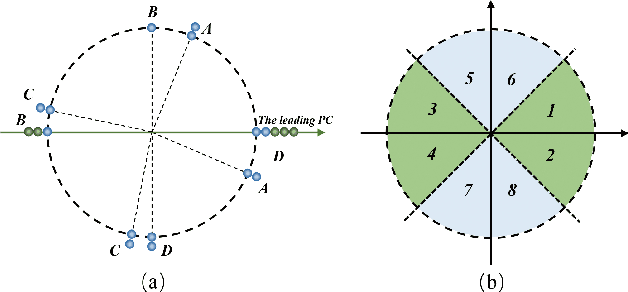
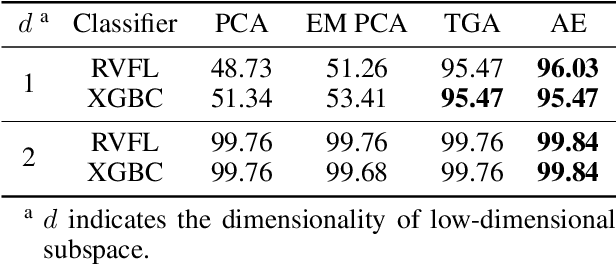
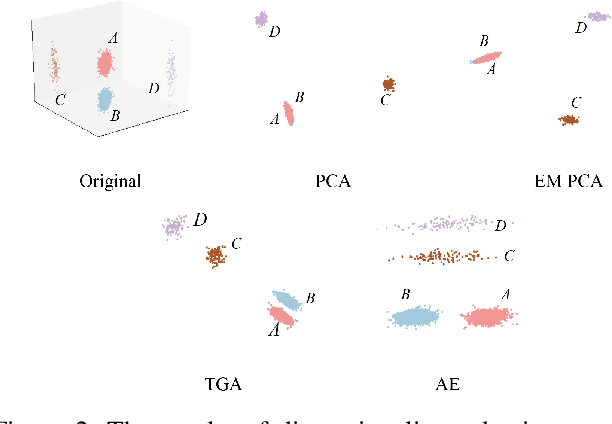
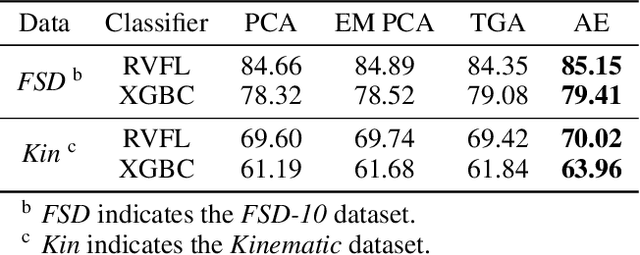
As a widely used method in machine learning, principal component analysis (PCA) shows excellent properties for dimensionality reduction. It is a serious problem that PCA is sensitive to outliers, which has been improved by numerous Robust PCA (RPCA) versions. However, the existing state-of-the-art RPCA approaches cannot easily remove or tolerate outliers by a non-iterative manner. To tackle this issue, this paper proposes Angular Embedding (AE) to formulate a straightforward RPCA approach based on angular density, which is improved for large scale or high-dimensional data. Furthermore, a trimmed AE (TAE) is introduced to deal with data with large scale outliers. Extensive experiments on both synthetic and real-world datasets with vector-level or pixel-level outliers demonstrate that the proposed AE/TAE outperforms the state-of-the-art RPCA based methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge