Analysis of spectral clustering algorithms for community detection: the general bipartite setting
Paper and Code
Mar 12, 2018
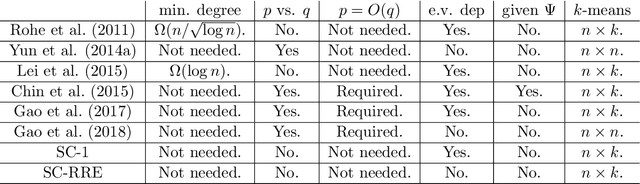

We consider the analysis of spectral clustering algorithms for community detection under a stochastic block model (SBM). A general spectral clustering algorithm consists of three steps: (1) regularization of an appropriate adjacency or Laplacian matrix (2) a form of spectral truncation and (3) a k-means type algorithm in the reduced spectral domain. By varying each step, one can obtain different spectral algorithms. In light of the recent developments in refining consistency results for the spectral clustering, we identify the necessary bounds at each of these three steps, and then derive and compare consistency results for some existing spectral algorithms as well as a new variant that we propose. The focus of the paper is on providing a better understanding of the analysis of spectral methods for community detection, with an emphasis on the bipartite setting which has received less theoretical consideration. We show how the variations in the spectral truncation step reflects in the consistency results under a general SBM. We also investigate the necessary bounds for the k-means step in some detail, allowing one to replace this step with any algorithm (k-means type or otherwise) that guarantees the necessary bound. We discuss some of the neglected aspects of the bipartite setting, e.g., the role of the mismatch between the communities of the two sides on the performance of spectral methods. Finally, we show how the consistency results can be extended beyond SBMs to the problem of clustering inhomogeneous random graph models that can be approximated by SBMs in a certain sense.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge