An Online-Learning Approach to Inverse Optimization
Paper and Code
Oct 30, 2018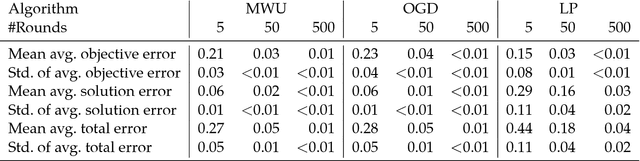
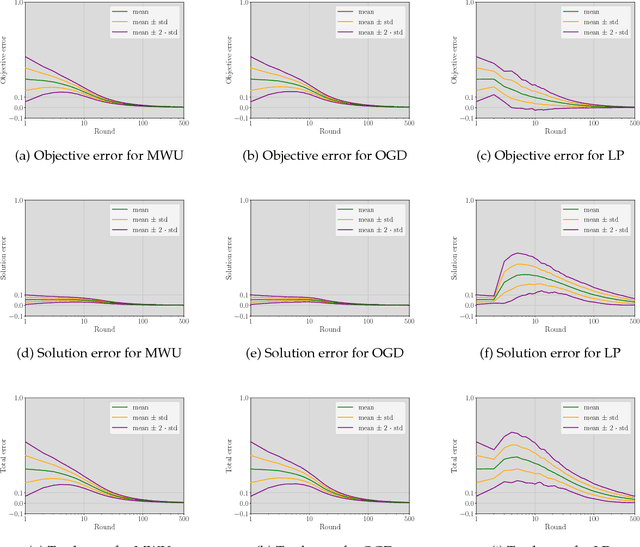

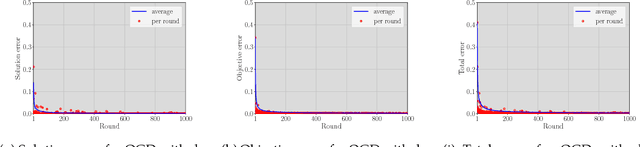
In this paper, we demonstrate how to learn the objective function of a decision-maker while only observing the problem input data and the decision-maker's corresponding decisions over multiple rounds. Our approach is based on online learning and works for linear objectives over arbitrary feasible sets for which we have a linear optimization oracle. As such, it generalizes previous approaches based on KKT-system decomposition and dualization. The two exact algorithms we present -- based on multiplicative weights updates and online gradient descent respectively -- converge at a rate of O(1/sqrt(T)) and thus allow taking decisions which are essentially as good as those of the observed decision-maker already after relatively few observations. We also discuss several useful generalizations, such as the approximate learning of non-linear objective functions and the case of suboptimal observations. Finally, we show the effectiveness and possible applications of our methods in a broad computational study.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge