An Iterative Closest Points Approach to Neural Generative Models
Paper and Code
Jul 02, 2018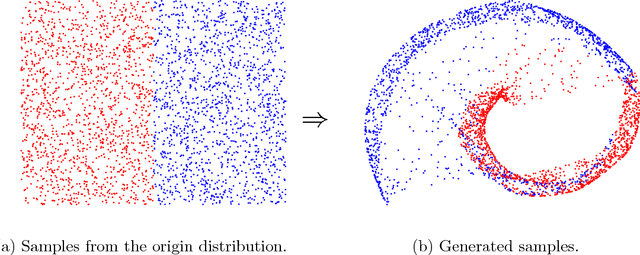
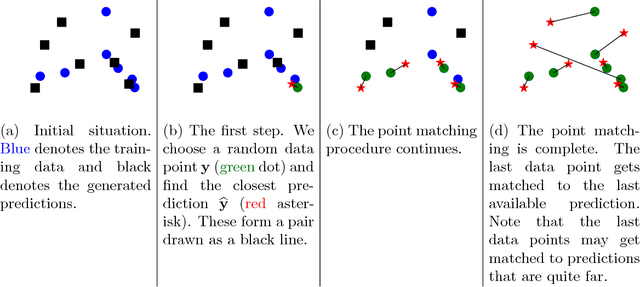
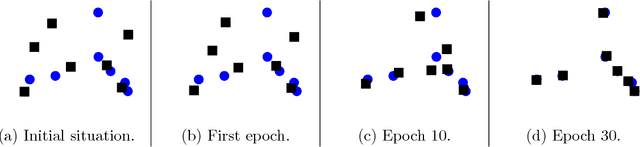
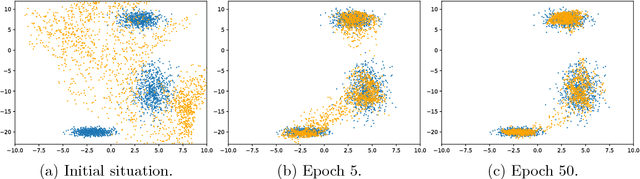
We present a simple way to learn a transformation that maps samples of one distribution to the samples of another distribution. Our algorithm comprises an iteration of 1) drawing samples from some simple distribution and transforming them using a neural network, 2) determining pairwise correspondences between the transformed samples and training data (or a minibatch), and 3) optimizing the weights of the neural network being trained to minimize the distances between the corresponding vectors. This can be considered as a variant of the Iterative Closest Points (ICP) algorithm, common in geometric computer vision, although ICP typically operates on sensor point clouds and linear transforms instead of random sample sets and neural nonlinear transforms. We demonstrate the algorithm on simple synthetic data and MNIST data. We furthermore demonstrate that the algorithm is capable of handling distributions with both continuous and discrete variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge