An Investigation into Mathematical Programming for Finite Horizon Decentralized POMDPs
Paper and Code
Jan 16, 2014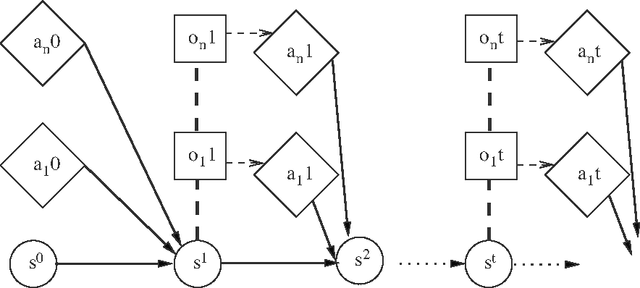
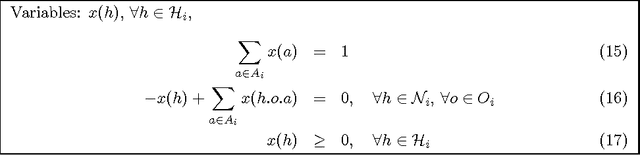
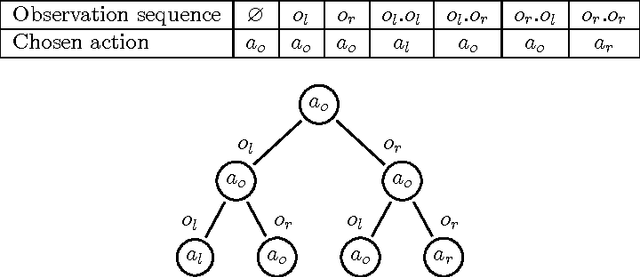
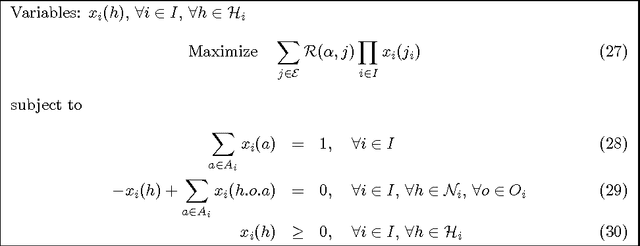
Decentralized planning in uncertain environments is a complex task generally dealt with by using a decision-theoretic approach, mainly through the framework of Decentralized Partially Observable Markov Decision Processes (DEC-POMDPs). Although DEC-POMDPS are a general and powerful modeling tool, solving them is a task with an overwhelming complexity that can be doubly exponential. In this paper, we study an alternate formulation of DEC-POMDPs relying on a sequence-form representation of policies. From this formulation, we show how to derive Mixed Integer Linear Programming (MILP) problems that, once solved, give exact optimal solutions to the DEC-POMDPs. We show that these MILPs can be derived either by using some combinatorial characteristics of the optimal solutions of the DEC-POMDPs or by using concepts borrowed from game theory. Through an experimental validation on classical test problems from the DEC-POMDP literature, we compare our approach to existing algorithms. Results show that mathematical programming outperforms dynamic programming but is less efficient than forward search, except for some particular problems. The main contributions of this work are the use of mathematical programming for DEC-POMDPs and a better understanding of DEC-POMDPs and of their solutions. Besides, we argue that our alternate representation of DEC-POMDPs could be helpful for designing novel algorithms looking for approximate solutions to DEC-POMDPs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge