An Extremal Optimization approach to parallel resonance constrained capacitor placement problem

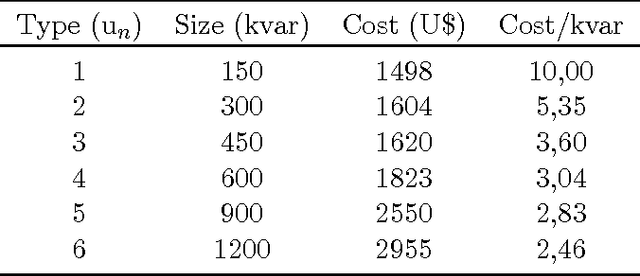
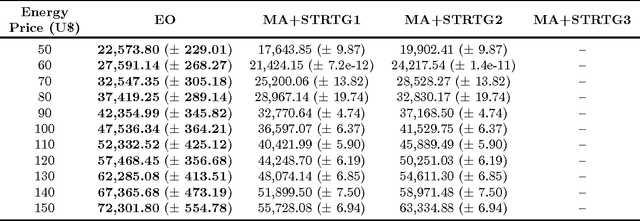
Installation of capacitors in distribution networks is one of the most used procedure to compensate reactive power generated by loads and, consequently, to reduce technical losses. So, the problem consists in identifying the optimal placement and sizing of capacitors. This problem is known in the literature as optimal capacitor placement problem. Neverthless, depending on the location and size of the capacitor, it may become a harmonic source, allowing capacitor to enter into resonance with the distribution network, causing several undesired side effects. In this work we propose a parsimonious method to deal with the capacitor placement problem that incorporates resonance constraints, ensuring that every allocated capacitor will not act as a harmonic source. This proposed algorithm is based upon a physical inspired metaheuristic known as Extremal Optimization. The results achieved showed that this proposal has reached significant gains when compared with other proposals that attempt repair, in a post-optimization stage, already obtained solutions which violate resonance constraints.