An Experimental Study of the Transferability of Spectral Graph Networks
Paper and Code
Dec 18, 2020

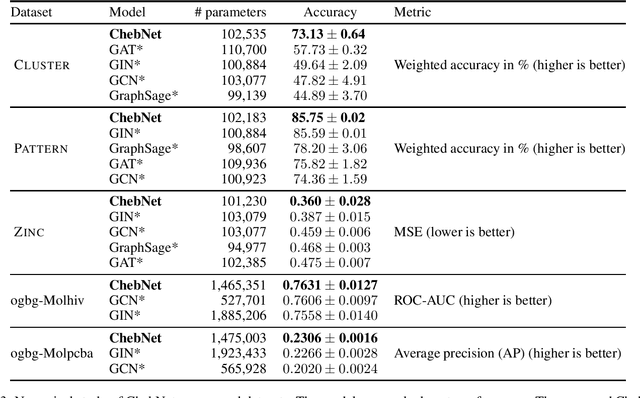
Spectral graph convolutional networks are generalizations of standard convolutional networks for graph-structured data using the Laplacian operator. A common misconception is the instability of spectral filters, i.e. the impossibility to transfer spectral filters between graphs of variable size and topology. This misbelief has limited the development of spectral networks for multi-graph tasks in favor of spatial graph networks. However, recent works have proved the stability of spectral filters under graph perturbation. Our work complements and emphasizes further the high quality of spectral transferability by benchmarking spectral graph networks on tasks involving graphs of different size and connectivity. Numerical experiments exhibit favorable performance on graph regression, graph classification, and node classification problems on two graph benchmarks. The implementation of our experiments is available on GitHub for reproducibility.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge