An Empirical Study of ADMM for Nonconvex Problems
Paper and Code
Dec 10, 2016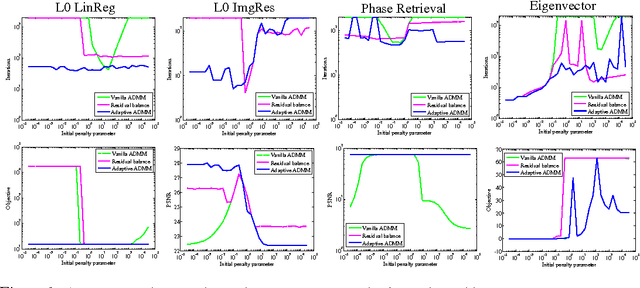
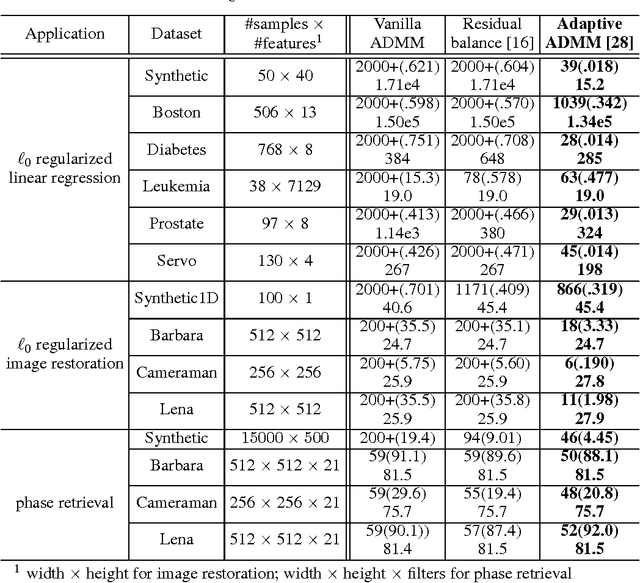
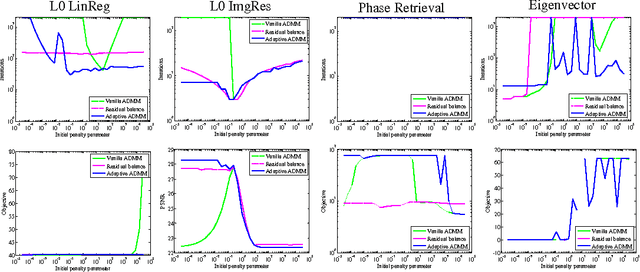
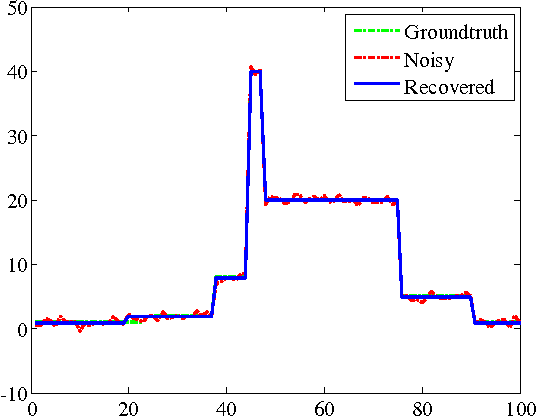
The alternating direction method of multipliers (ADMM) is a common optimization tool for solving constrained and non-differentiable problems. We provide an empirical study of the practical performance of ADMM on several nonconvex applications, including l0 regularized linear regression, l0 regularized image denoising, phase retrieval, and eigenvector computation. Our experiments suggest that ADMM performs well on a broad class of non-convex problems. Moreover, recently proposed adaptive ADMM methods, which automatically tune penalty parameters as the method runs, can improve algorithm efficiency and solution quality compared to ADMM with a non-tuned penalty.
* NIPS nonconvex workshop
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge