An Efficient Triplet-based Algorithm for Evidential Reasoning

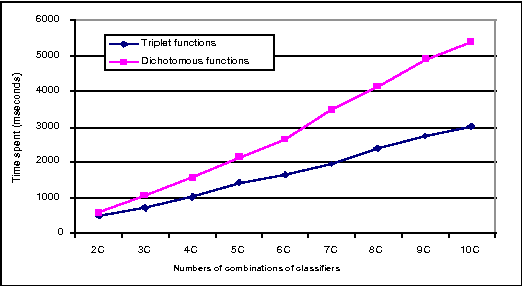
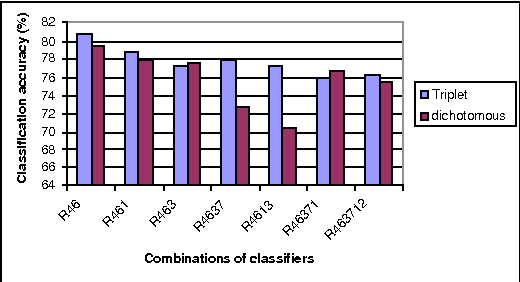
Linear-time computational techniques have been developed for combining evidence which is available on a number of contending hypotheses. They offer a means of making the computation-intensive calculations involved more efficient in certain circumstances. Unfortunately, they restrict the orthogonal sum of evidential functions to the dichotomous structure applies only to elements and their complements. In this paper, we present a novel evidence structure in terms of a triplet and a set of algorithms for evidential reasoning. The merit of this structure is that it divides a set of evidence into three subsets, distinguishing trivial evidential elements from important ones focusing some particular elements. It avoids the deficits of the dichotomous structure in representing the preference of evidence and estimating the basic probability assignment of evidence. We have established a formalism for this structure and the general formulae for combining pieces of evidence in the form of the triplet, which have been theoretically justified.