An Efficient Smoothing Proximal Gradient Algorithm for Convex Clustering
Paper and Code
Jun 22, 2020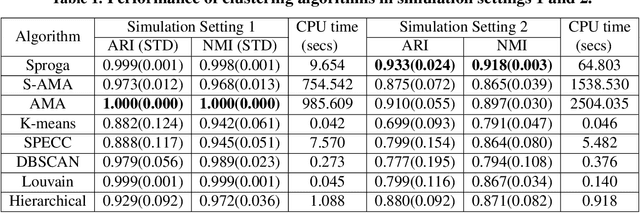
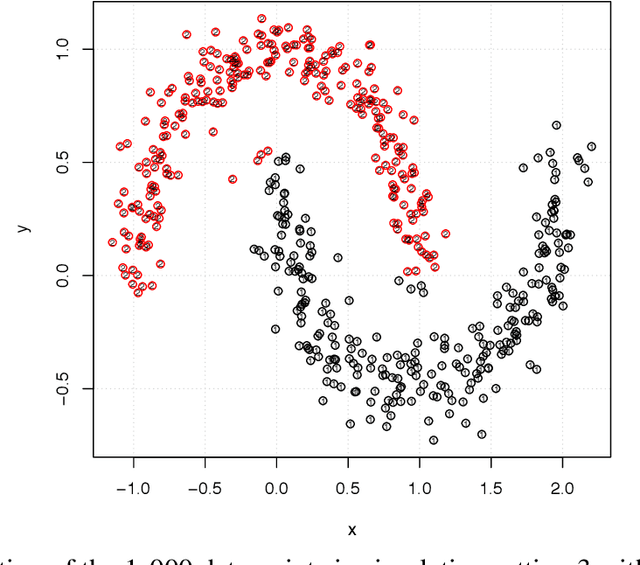
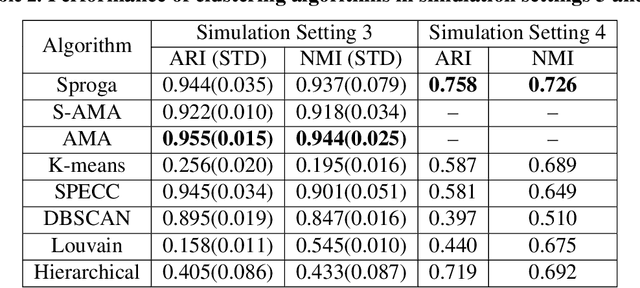
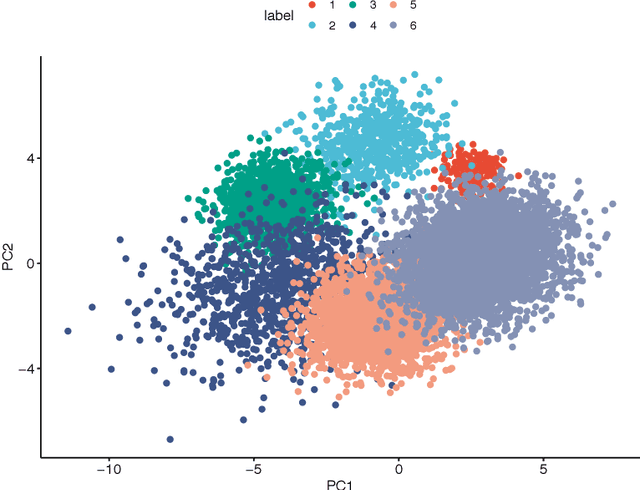
Cluster analysis organizes data into sensible groupings and is one of fundamental modes of understanding and learning. The widely used K-means and hierarchical clustering methods can be dramatically suboptimal due to local minima. Recently introduced convex clustering approach formulates clustering as a convex optimization problem and ensures a globally optimal solution. However, the state-of-the-art convex clustering algorithms, based on the alternating direction method of multipliers (ADMM) or the alternating minimization algorithm (AMA), require large computation and memory space, which limits their applications. In this paper, we develop a very efficient smoothing proximal gradient algorithm (Sproga) for convex clustering. Our Sproga is faster than ADMM- or AMA-based convex clustering algorithms by one to two orders of magnitude. The memory space required by Sproga is less than that required by ADMM and AMA by at least one order of magnitude. Computer simulations and real data analysis show that Sproga outperforms several well known clustering algorithms including K-means and hierarchical clustering. The efficiency and superior performance of our algorithm will help convex clustering to find its wide application.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge