An efficient iterative thresholding method for image segmentation
Paper and Code
Aug 12, 2016
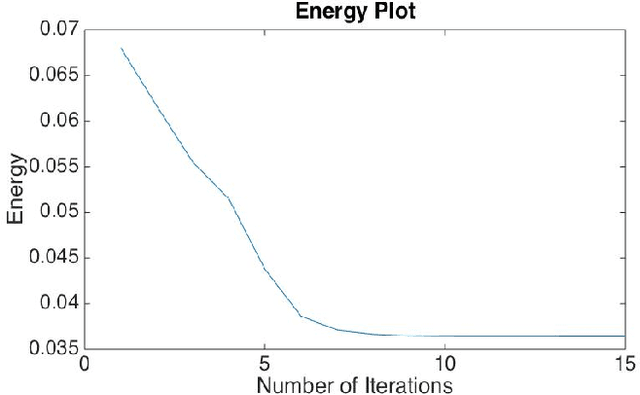
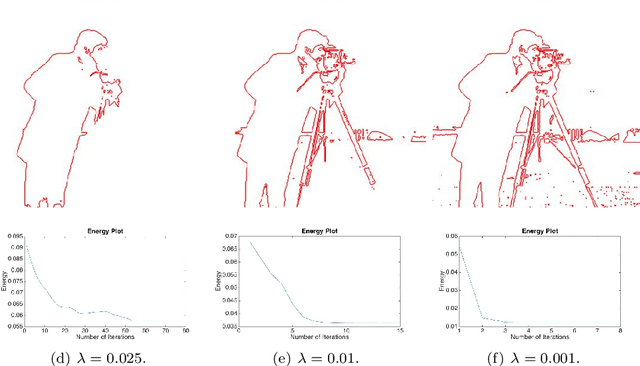
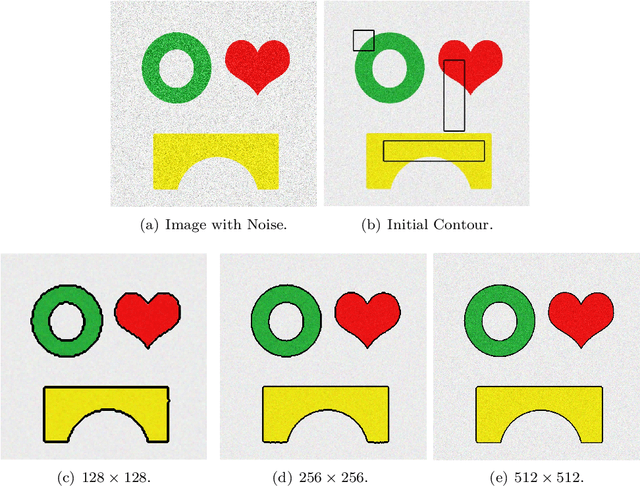
We proposed an efficient iterative thresholding method for multi-phase image segmentation. The algorithm is based on minimizing piecewise constant Mumford-Shah functional in which the contour length (or perimeter) is approximated by a non-local multi-phase energy. The minimization problem is solved by an iterative method. Each iteration consists of computing simple convolutions followed by a thresholding step. The algorithm is easy to implement and has the optimal complexity $O(N \log N)$ per iteration. We also show that the iterative algorithm has the total energy decaying property. We present some numerical results to show the efficiency of our method.
* 14 pages, 21 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge