An Application of Manifold Learning in Global Shape Descriptors
Paper and Code
Jan 08, 2019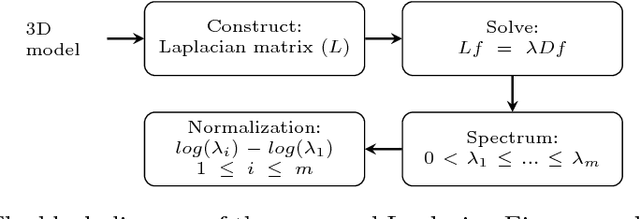
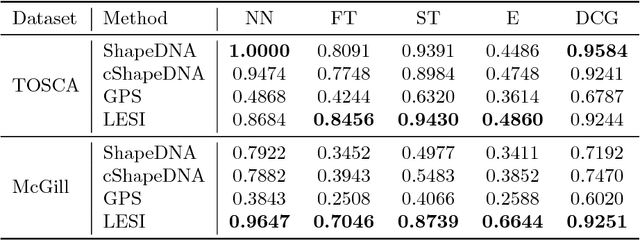
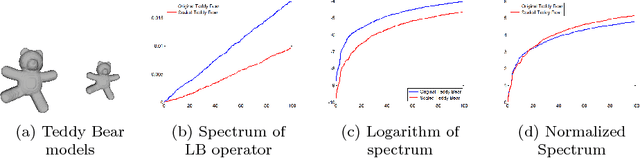

With the rapid expansion of applied 3D computational vision, shape descriptors have become increasingly important for a wide variety of applications and objects from molecules to planets. Appropriate shape descriptors are critical for accurate (and efficient) shape retrieval and 3D model classification. Several spectral-based shape descriptors have been introduced by solving various physical equations over a 3D surface model. In this paper, for the first time, we incorporate a specific group of techniques in statistics and machine learning, known as manifold learning, to develop a global shape descriptor in the computer graphics domain. The proposed descriptor utilizes the Laplacian Eigenmap technique in which the Laplacian eigenvalue problem is discretized using an exponential weighting scheme. As a result, our descriptor eliminates the limitations tied to the existing spectral descriptors, namely dependency on triangular mesh representation and high intra-class quality of 3D models. We also present a straightforward normalization method to obtain a scale-invariant descriptor. The extensive experiments performed in this study show that the present contribution provides a highly discriminative and robust shape descriptor under the presence of a high level of noise, random scale variations, and low sampling rate, in addition to the known isometric-invariance property of the Laplace-Beltrami operator. The proposed method significantly outperforms state-of-the-art algorithms on several non-rigid shape retrieval benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge