An Analysis of the Expressiveness of Deep Neural Network Architectures Based on Their Lipschitz Constants
Paper and Code
Dec 24, 2019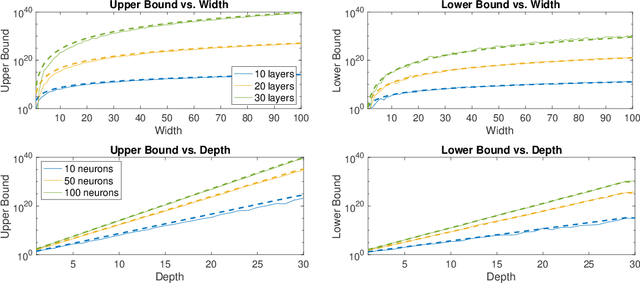

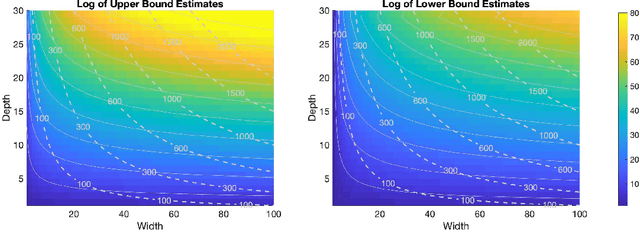

Deep neural networks (DNNs) have emerged as a popular mathematical tool for function approximation due to their capability of modelling highly nonlinear functions. Their applications range from image classification and natural language processing to learning-based control. Despite their empirical successes, there is still a lack of theoretical understanding of the representative power of such deep architectures. In this work, we provide a theoretical analysis of the expressiveness of fully-connected, feedforward DNNs with 1-Lipschitz activation functions. In particular, we characterize the expressiveness of a DNN by its Lipchitz constant. By leveraging random matrix theory, we show that, given sufficiently large and randomly distributed weights, the expected upper and lower bounds of the Lipschitz constant of a DNN and hence their expressiveness increase exponentially with depth and polynomially with width, which gives rise to the benefit of the depth of DNN architectures for efficient function approximation. This observation is consistent with established results based on alternative expressiveness measures of DNNs. In contrast to most of the existing work, our analysis based on the Lipschitz properties of DNNs is applicable to a wider range of activation nonlinearities and potentially allows us to make sensible comparisons between the complexity of a DNN and the function to be approximated by the DNN. We consider this work to be a step towards understanding the expressive power of DNNs and towards designing appropriate deep architectures for practical applications such as system control.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge