An Algebra to Merge Heterogeneous Classifiers
Paper and Code
Jan 22, 2015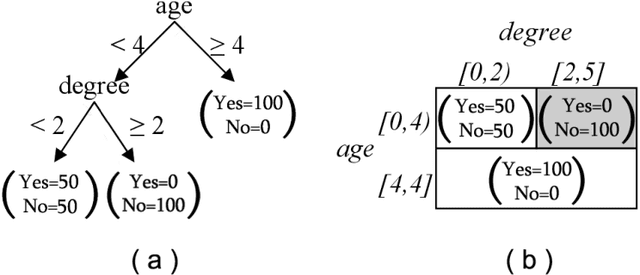
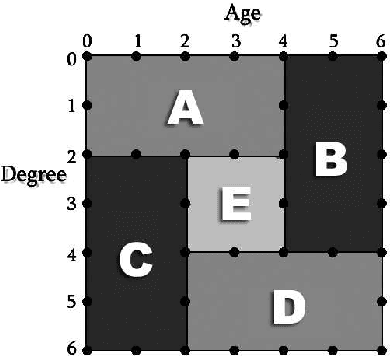
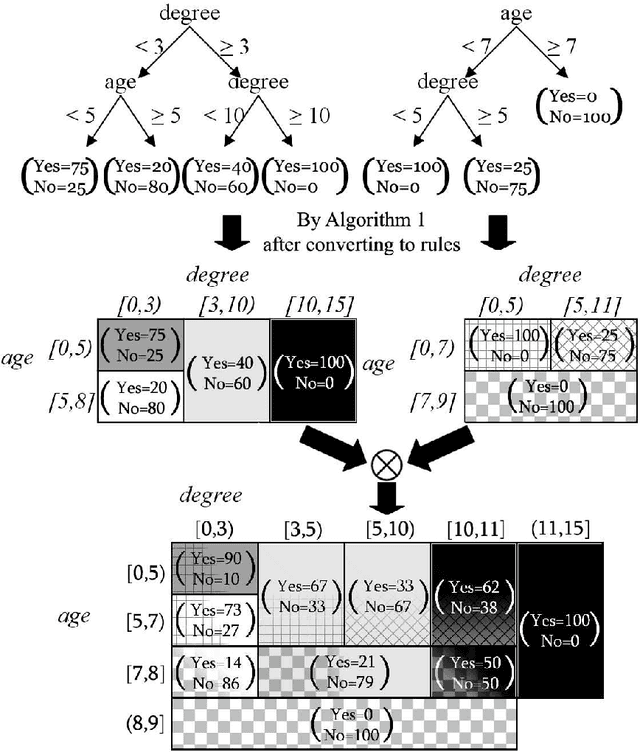
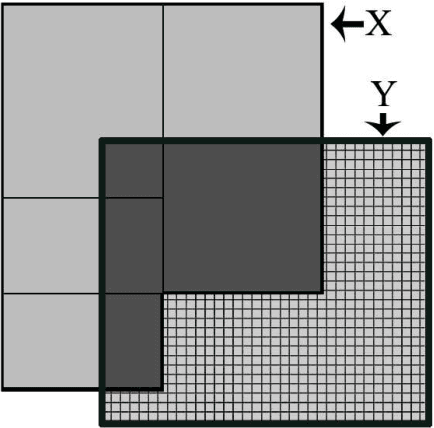
In distributed classification, each learner observes its environment and deduces a classifier. As a learner has only a local view of its environment, classifiers can be exchanged among the learners and integrated, or merged, to improve accuracy. However, the operation of merging is not defined for most classifiers. Furthermore, the classifiers that have to be merged may be of different types in settings such as ad-hoc networks in which several generations of sensors may be creating classifiers. We introduce decision spaces as a framework for merging possibly different classifiers. We formally study the merging operation as an algebra, and prove that it satisfies a desirable set of properties. The impact of time is discussed for the two main data mining settings. Firstly, decision spaces can naturally be used with non-stationary distributions, such as the data collected by sensor networks, as the impact of a model decays over time. Secondly, we introduce an approach for stationary distributions, such as homogeneous databases partitioned over different learners, which ensures that all models have the same impact. We also present a method that uses storage flexibly to achieve different types of decay for non-stationary distributions. Finally, we show that the algebraic approach developed for merging can also be used to analyze the behaviour of other operators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge