Alpha-Beta Divergence For Variational Inference
Paper and Code
May 20, 2018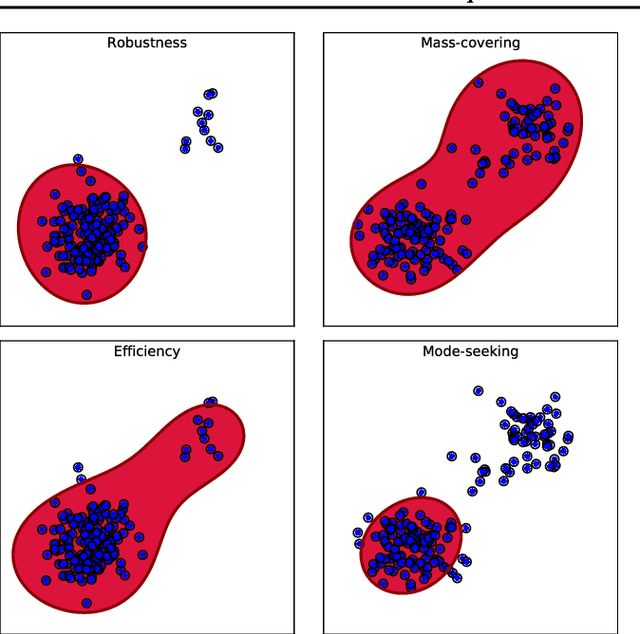
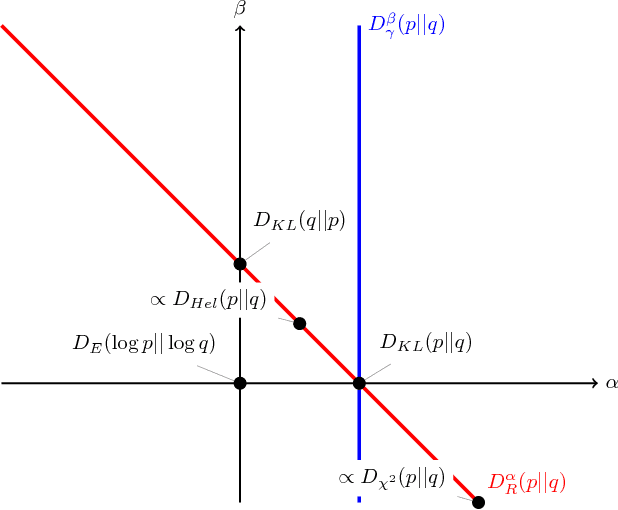
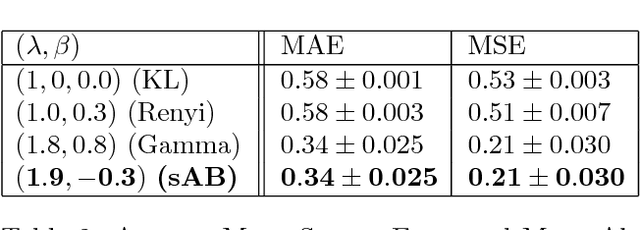
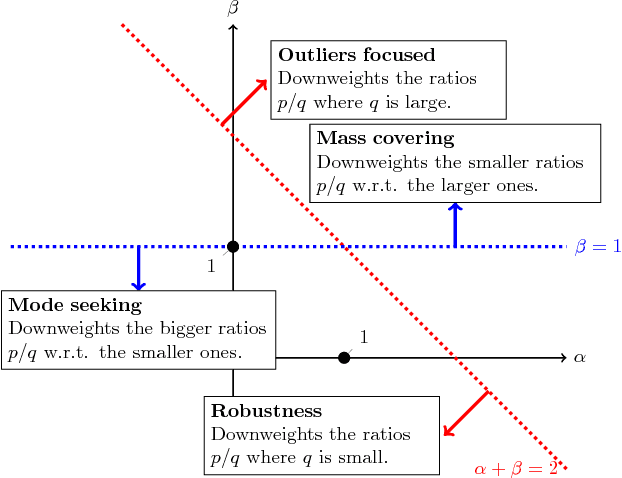
This paper introduces a variational approximation framework using direct optimization of what is known as the {\it scale invariant Alpha-Beta divergence} (sAB divergence). This new objective encompasses most variational objectives that use the Kullback-Leibler, the R{\'e}nyi or the gamma divergences. It also gives access to objective functions never exploited before in the context of variational inference. This is achieved via two easy to interpret control parameters, which allow for a smooth interpolation over the divergence space while trading-off properties such as mass-covering of a target distribution and robustness to outliers in the data. Furthermore, the sAB variational objective can be optimized directly by repurposing existing methods for Monte Carlo computation of complex variational objectives, leading to estimates of the divergence instead of variational lower bounds. We show the advantages of this objective on Bayesian models for regression problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge