Algorithmic Bias and Data Bias: Understanding the Relation between Distributionally Robust Optimization and Data Curation
Paper and Code
Jun 17, 2021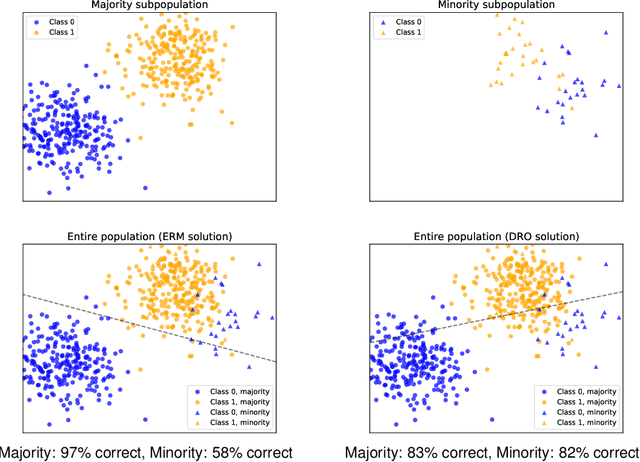
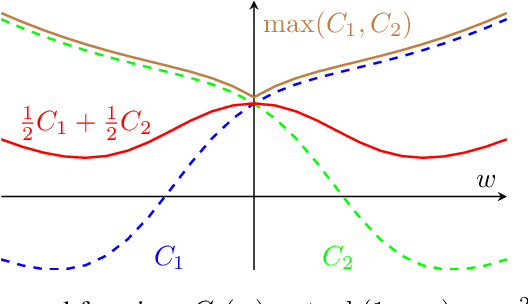
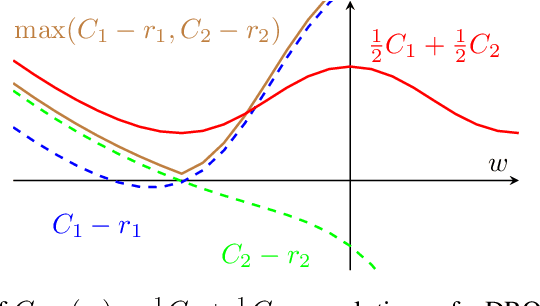
Machine learning systems based on minimizing average error have been shown to perform inconsistently across notable subsets of the data, which is not exposed by a low average error for the entire dataset. In consequential social and economic applications, where data represent people, this can lead to discrimination of underrepresented gender and ethnic groups. Given the importance of bias mitigation in machine learning, the topic leads to contentious debates on how to ensure fairness in practice (data bias versus algorithmic bias). Distributionally Robust Optimization (DRO) seemingly addresses this problem by minimizing the worst expected risk across subpopulations. We establish theoretical results that clarify the relation between DRO and the optimization of the same loss averaged on an adequately weighted training dataset. The results cover finite and infinite number of training distributions, as well as convex and non-convex loss functions. We show that neither DRO nor curating the training set should be construed as a complete solution for bias mitigation: in the same way that there is no universally robust training set, there is no universal way to setup a DRO problem and ensure a socially acceptable set of results. We then leverage these insights to provide a mininal set of practical recommendations for addressing bias with DRO. Finally, we discuss ramifications of our results in other related applications of DRO, using an example of adversarial robustness. Our results show that there is merit to both the algorithm-focused and the data-focused side of the bias debate, as long as arguments in favor of these positions are precisely qualified and backed by relevant mathematics known today.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge