Adversarially Robust Out-of-Distribution Detection Using Lyapunov-Stabilized Embeddings
Paper and Code
Oct 14, 2024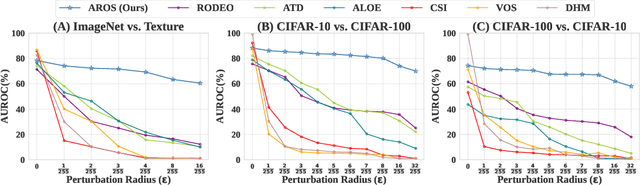
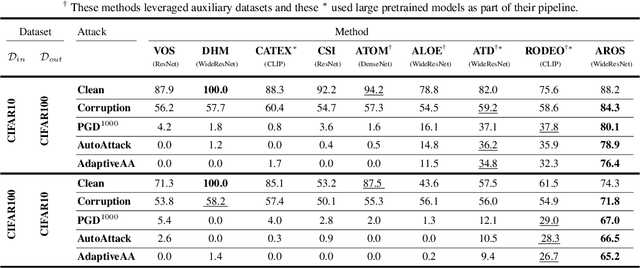
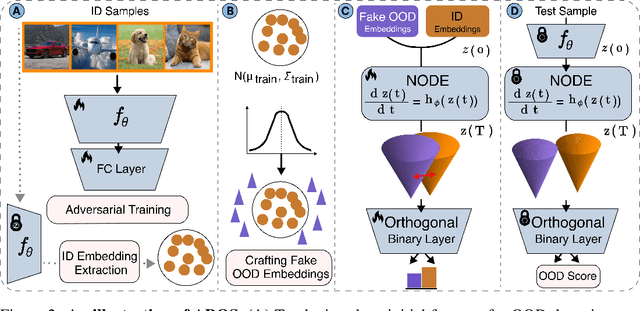
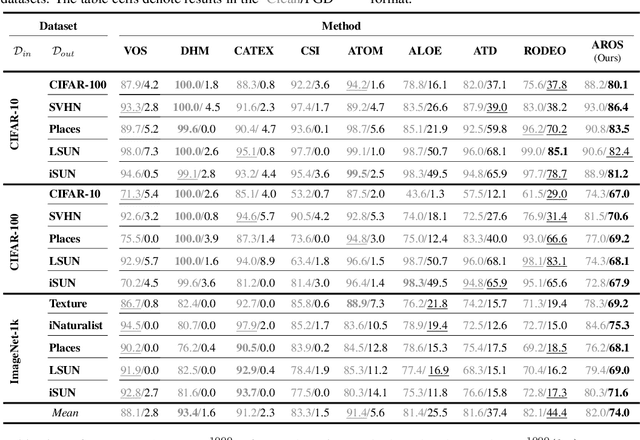
Despite significant advancements in out-of-distribution (OOD) detection, existing methods still struggle to maintain robustness against adversarial attacks, compromising their reliability in critical real-world applications. Previous studies have attempted to address this challenge by exposing detectors to auxiliary OOD datasets alongside adversarial training. However, the increased data complexity inherent in adversarial training, and the myriad of ways that OOD samples can arise during testing, often prevent these approaches from establishing robust decision boundaries. To address these limitations, we propose AROS, a novel approach leveraging neural ordinary differential equations (NODEs) with Lyapunov stability theorem in order to obtain robust embeddings for OOD detection. By incorporating a tailored loss function, we apply Lyapunov stability theory to ensure that both in-distribution (ID) and OOD data converge to stable equilibrium points within the dynamical system. This approach encourages any perturbed input to return to its stable equilibrium, thereby enhancing the model's robustness against adversarial perturbations. To not use additional data, we generate fake OOD embeddings by sampling from low-likelihood regions of the ID data feature space, approximating the boundaries where OOD data are likely to reside. To then further enhance robustness, we propose the use of an orthogonal binary layer following the stable feature space, which maximizes the separation between the equilibrium points of ID and OOD samples. We validate our method through extensive experiments across several benchmarks, demonstrating superior performance, particularly under adversarial attacks. Notably, our approach improves robust detection performance from 37.8% to 80.1% on CIFAR-10 vs. CIFAR-100 and from 29.0% to 67.0% on CIFAR-100 vs. CIFAR-10.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge