ADMM and Spectral Proximity Operators in Hyperspectral Broadband Phase Retrieval for Quantitative Phase Imaging
Paper and Code
May 14, 2021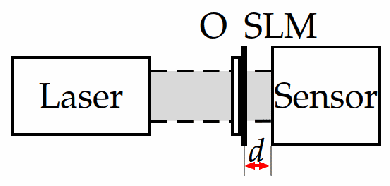
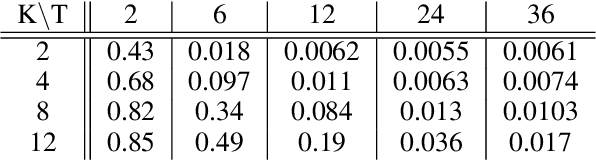

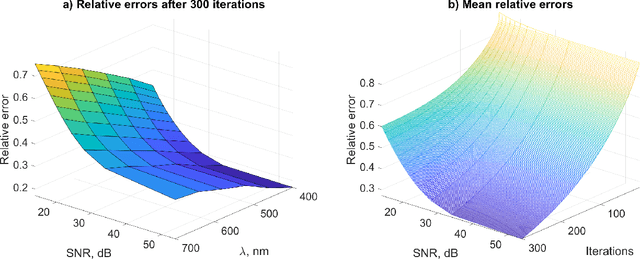
A novel formulation of the hyperspectral broadband phase retrieval is developed for the scenario where both object and modulation phase masks are spectrally varying. The proposed algorithm is based on a complex domain version of the alternating direction method of multipliers (ADMM) and Spectral Proximity Operators (SPO) derived for Gaussian and Poissonian observations. Computations for these operators are reduced to the solution of sets of cubic (for Gaussian) and quadratic (for Poissonian) algebraic equations. These proximity operators resolve two problems. Firstly, the complex domain spectral components of signals are extracted from the total intensity observations calculated as sums of the signal spectral intensities. In this way, the spectral analysis of the total intensities is achieved. Secondly, the noisy observations are filtered, compromising noisy intensity observations and their predicted counterparts. The ability to resolve the hyperspectral broadband phase retrieval problem and to find the spectrum varying object are essentially defined by the spectral properties of object and image formation operators. The simulation tests demonstrate that the phase retrieval in this formulation can be successfully resolved.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge