Addressing Unboundedness in Quadratically-Constrained Mixed-Integer Problems
Paper and Code
May 06, 2024
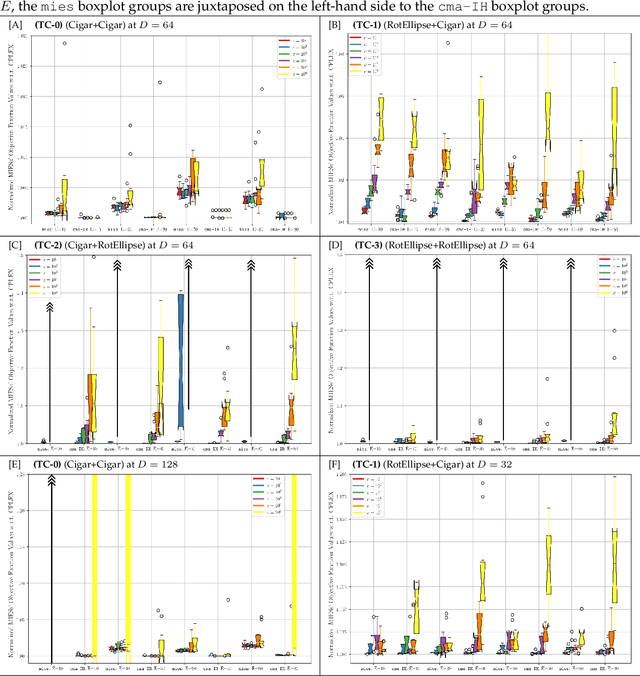
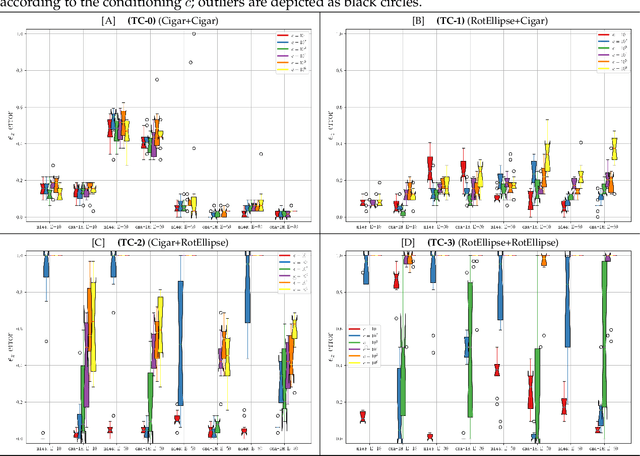
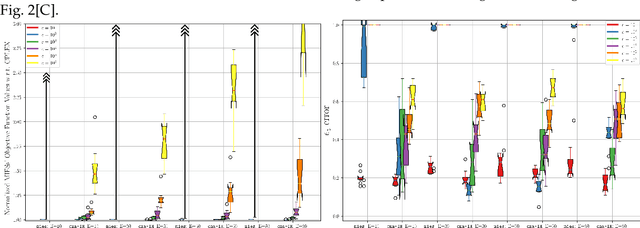
Quadratically-constrained unbounded integer programs hold the distinction of being undecidable, suggesting a possible soft-spot for Mathematical Programming (MP) techniques, which otherwise constitute a good choice to treat integer or mixed-integer (MI) problems. We consider the challenge of minimizing MI convex quadratic objective functions subject to unbounded decision variables and quadratic constraints. Given the theoretical weakness of white-box MP solvers to handle such models, we turn to black-box meta-heuristics of the Evolution Strategies (ESs) family, and question their capacity to solve this challenge. Through an empirical assessment of quadratically-constrained quadratic objective functions, across varying Hessian forms and condition numbers, we compare the performance of the CPLEX solver to state-of-the-art MI ESs, which handle constraints by penalty. Our systematic investigation begins where the CPLEX solver encounters difficulties (timeouts as the search-space dimensionality increases, (D>=30), on which we report by means of detailed analyses. Overall, the empirical observations confirm that black-box and white-box solvers can be competitive, especially when the constraint function is separable, and that two common ESs' mutation operators can effectively handle the integer unboundedness. We also conclude that conditioning and separability are not intuitive factors in determining the complexity of this class of MI problems, where regular versus rough landscape structures can pose mirrored degrees of challenge for MP versus ESs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge